
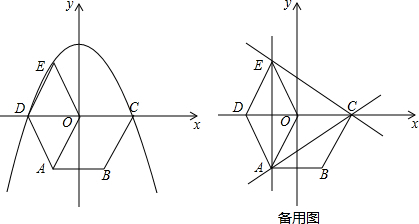
分析 (1)如图1中,连接OB,作EM⊥OD于M,首先说明点D在x轴上,再求出OM、EM的长即可解决问题.
(2)因为C与D关于y轴对称,所以抛物线的对称轴为y轴,推出b=0,再利用待定系数法即可解决.
(4)如图2中,P1(0,0)是△ACE的内心,P1,P2,P3是△ACE的外角平分线的交点.则P1、P2、P3、P4到△ACE三边距离相等.分别求出坐标即可.
解答 解:(1)如图1中,连接OB,作EM⊥OD于M.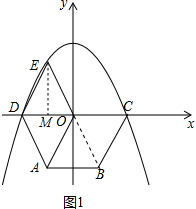
∵四边形ABCD是菱形,
∴OA=AB=OC=BC=2,
∵∠OAB=60°,
∴△OAB,△OBC是等边三角形,
∴∠AOB=∠BOC=∠AOD=60°,
∵四边形AOED是由四边形OABC沿OA翻折得到,
∴点D在x轴上,OD=DE=EO=2,
在RT△EOM中,∵∠∠EMO=90°,∠MEO=30°,EO=2,
∴MO=1,EM=$\sqrt{3}$,
∴点D坐标(-2,0),点E坐标(-1,$\sqrt{3}$).
(2)∵C(2,0),D(-2,0),
∴C与D关于y轴对称,
∴抛物线的对称轴为y轴,即$-\frac{b}{2a}=0$
∴b=0,
把C(或D)与E的坐标代入y=ax2+c得$\left\{\begin{array}{l}{4a+c=0}\\{a+c=\sqrt{3}}\end{array}\right.$
解得$a=-\frac{{\sqrt{3}}}{3}$,$c=\frac{{4\sqrt{3}}}{3}$,
∴抛物线的解析式为$y=-\frac{{\sqrt{3}}}{3}{x^2}+\frac{{4\sqrt{3}}}{3}$.
(3)如图2中,P1(0,0)是△ACE的内心,P1,P2,P3是△ACE的外角平分线的交点.则P1、P2、P3、P4到△ACE三边距离相等.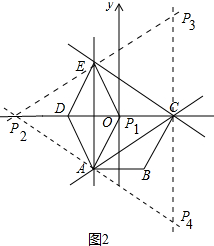
由(1)可知,△ACE是等边三角形,
∠P3EC=∠P3CE=60°,
∴△P3EC是等边三角形,同理△P2AE,△P4AC都是等边三角形且边长都是2$\sqrt{3}$,
∵P3P4⊥OC,
∴P3(2,$2\sqrt{3}$),P4(2,$-2\sqrt{3}$),
∵OP2=4,
∴P1(0,0),P2(-4,0).
综上所述满足条件的点P的坐标P1(0,0),P2(-4,0),P3(2,$2\sqrt{3}$),P4(2,$-2\sqrt{3}$).
点评 本题考查二次函数综合题、角平分线的性质、等边三角形的性质、菱形的性质等知识,解题的关键是熟练掌握待定系数法、记住到角的两边距离相等的点在这个角的平分线上,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )
吴磊在如图所示的某校的平面示意图中建立平面直角坐标系,若表示图书馆位置的点A和表示食堂位置的点B都在x轴上,且关于y轴对称,则表示教学楼位置的点C的坐标是( )| A. | (1,-2) | B. | (-1,2) | C. | (-1,-2) | D. | (-1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
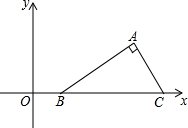 如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )
如图,在平面直角坐标系中Rt△ABC的斜边BC在x轴上,点B坐标为(1,0),AC=2,∠ABC=30°,把Rt△ABC先绕B点顺时针旋转180°,然后再向下平移2个单位,则A点的对应点A′的坐标为( )| A. | (-4,-2-$\sqrt{3}$) | B. | (-4,-2+$\sqrt{3}$) | C. | (-2,-2+$\sqrt{3}$) | D. | (-2,-2-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售方式 | 粗加工后销售 | 精加工后销售 |
| 每吨获利(元) | 1000 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO.
如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE•PO.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).
矩形ABCD中,AC是对角线,AB=$\sqrt{3}$,将△ABC绕点C顺时针旋转60°,点B恰好落在AD边上的点E处,点A经过的路径是$\widehat{AF}$,则图中影阴部分的面积为$\frac{7}{6}π$-$\frac{3}{2}\sqrt{3}$.(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
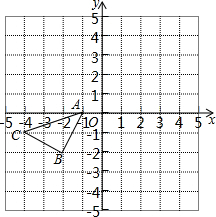 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com