
分析 (1)由红球的个数以及袋子中球的总数目即可求出搅匀后从中任意摸出1个球,恰好是红球的概率;
(2)化树状图得出所有等可能的情况数,找出两次都是红球的情况数,即可求出所求的概率.
解答 解:
(1)∵一只不透明的袋子中装有颜色分别为红、黄、蓝的球各一个,
∴从中任意摸出1个球,恰好是红球的概率=$\frac{1}{3}$,
故答案为:$\frac{1}{3}$;
(2)画树状图得: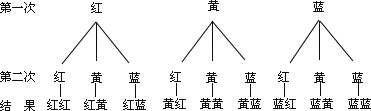
∴P(两次都是摸到红球)=$\frac{1}{9}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
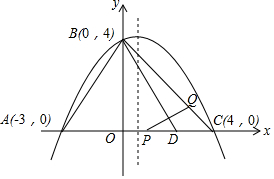 如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.
如图:抛物线经过A(-3,0)、B(0,4)、C(4,0)三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
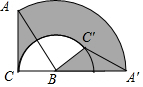 如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )
如图,将斜边长为4,∠A为30°角的Rt△ABC绕点B顺时针旋转120°得到△A′C′B,弧$\widehat{AA′}$、$\widehat{CC′}$是旋转过程中A、C的运动轨迹,则图中阴影部分的面积为( )| A. | 4π+2$\sqrt{3}$ | B. | $\frac{16}{3}$π-2$\sqrt{3}$ | C. | $\frac{16}{3}$π+2$\sqrt{3}$ | D. | 4π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
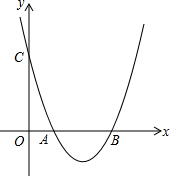 已知二次函数y=a(x-1)(x-3)(a>0)的图象与x轴交于A、B两点(A左B右),与y轴交于C点(0,3).P为x轴下方二次函数y=a(x-1)(x-3)(a>0)图象上一点,P点横坐标为m.
已知二次函数y=a(x-1)(x-3)(a>0)的图象与x轴交于A、B两点(A左B右),与y轴交于C点(0,3).P为x轴下方二次函数y=a(x-1)(x-3)(a>0)图象上一点,P点横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
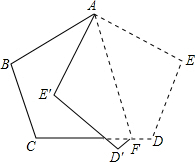 将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在E′,D′点.已知∠AFC=76°,则∠CFD′等于( )
将五边形纸片ABCDE按如图方式折叠,折痕为AF,点E,D分别落在E′,D′点.已知∠AFC=76°,则∠CFD′等于( )| A. | 15° | B. | 25° | C. | 28° | D. | 31° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com