
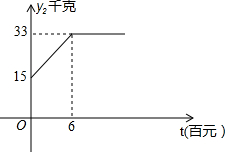
 茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).
茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).| 型号 | A型包装 | B型包装 | C型包装 |
| 每盒装 | 龙井1千克 | 毛尖1千克 | 毛尖0.4千克;龙井0.6千克 |
| 每盒价格 | 45元 | 60元 | 56元 |
分析 (1)直接将张大爷每亩丘陵地投资6(百元)时,代入解析式即可求出每亩产量,进而求出总产量;
(2)根据x的取值范围是w,分别求出解析式相加即可;
(3)根据二次函数的对称轴得出最值,再根据公式求出最值即可;
(4)设安排C型包装m盒,则A型包装(885-0.6)盒,B型包装(700-0.4)盒.设可获利润Z元.由利润=销售总价格-总投资资金就可以表示出Z与m的关系式即可.
解答 解:(1)由图象知y2=$\left\{\begin{array}{l}{3x+15(0≤x≤6)}\\{33(x>6)}\end{array}\right.$
∵20x+30t=240
∴当x=6时,t=4;
当t=6时,x=3,
因此,每亩丘陵地投资600元时,茶叶总产量为:20×[-$\frac{1}{4}$(6-8)2+36]+30(3×4+15)=1510(千克);
每亩山地投资600元时,茶叶总产量为:20×[-$\frac{1}{4}$(3-8)2+36]+30(3×6+15)=1585(千克);
(2)由20x+30t-240得t=8-$\frac{2}{3}$x.
①由$\left\{\begin{array}{l}{0≤x≤6}\\{0≤8-\frac{2}{3}x≤6}\end{array}\right.$得3≤x≤6;W=20×[-$\frac{1}{4}$(x-8)2+36]+30[(8-$\frac{2}{3}$x)+15]=-5(x-2)2+1590;
②由$\left\{\begin{array}{l}{0≤x≤6}\\{8-\frac{2}{3}x>6}\end{array}\right.$得0≤x<3,W=20×[-$\frac{1}{4}$(x-8)2+36]+30×33=5(x-8)2+1710;
③由$\left\{\begin{array}{l}{x>6}\\{0≤8-\frac{2}{3}x≤6}\end{array}\right.$得6<x≤12,W=35×20+30×[3(8-$\frac{2}{3}$x)+15]=-60x+1870;
④由$\left\{\begin{array}{l}{x>6}\\{8-\frac{2}{3}x>6}\end{array}\right.$,此不等式组无解.
(3)由(2)中①得,当x=3时,W最大=1585,由(2)中②得,当x=3时,W最大=1585
由(2)中③得,当x=6时,W最大=1510.
故当x=3(百元)时,茶叶总产量最高,最高产量是1585千克.
(4)龙井:1585-700=885千克,
设安排C型包装m盒,则A型包装(885-0.6)盒,B型包装(700-0.4)盒.
设可获利润Z元.依题意知:Z=45(885-0.6m)+60(700-0.4m)+56m-24000=5m+57825.
∵5>0,
∴Z随m的增大而增大,
又 m≥0,且885-0.6m≥0;且700-0.4m≥0.
∴0≤m≤1475,且m为整数.
∴当m=1475时,Z最大=65200,885-0.6m=0,700-0.4m=110.
即安排A型包装0盒,B型包装110盒,C型包装1475盒,利润最大,为65200元.
点评 本题考查了一元一次不等式组的运用,分类讨论的运用,二次函数的解析式的运用,一次函数的解析式的运用,函数的性质的运用,解答时求出函数的解析式是关键.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 若a2=b2,则a=b | B. | 若a>b,则a2>b2 | ||
| C. | 若a≠0,b≠0,则a2+b2>0 | D. | 若a≠b,则a2≠b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
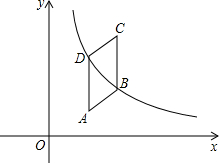 如图,在?ABCD中,AB⊥BD,sinA=$\frac{4}{5}$,将?ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=$\frac{k}{x}$(k>0)同时经过B、D两点,则点B的坐标是($\frac{9}{5}$,$\frac{4}{3}$).
如图,在?ABCD中,AB⊥BD,sinA=$\frac{4}{5}$,将?ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=$\frac{k}{x}$(k>0)同时经过B、D两点,则点B的坐标是($\frac{9}{5}$,$\frac{4}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根
矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根查看答案和解析>>
科目:初中数学 来源: 题型:解答题
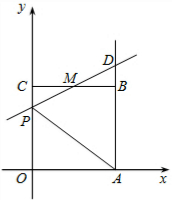
 己知如图,在梯形ABCD中,AB∥CD.AC、BD为对角线,MN∥CB.且与AB、DC分别相交于点M、N.与DB、AC分别相交于点P、Q.
己知如图,在梯形ABCD中,AB∥CD.AC、BD为对角线,MN∥CB.且与AB、DC分别相交于点M、N.与DB、AC分别相交于点P、Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB<AD,AF⊥BD于点E,交BC于点F,连接DF,则下列结论错误的是( )
如图,在矩形ABCD中,AB<AD,AF⊥BD于点E,交BC于点F,连接DF,则下列结论错误的是( )| A. | △ABC≌△CDB | B. | S△ABD=S△ADF | C. | ∠ADB=∠CDF | D. | ∠DBF>∠BDF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com