
【题目】如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE= ![]() AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.
AD(n为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG.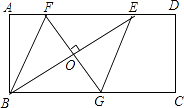
(1)试判断四边形BFEG的形状,并说明理由;
(2)当AB=a(a为常数),n=3时,求FG的长;
(3)记四边形BFEG的面积为S1 , 矩形ABCD的面积为S2 , 当 ![]() =
= ![]() 时,求n的值.(直接写出结果,不必写出解答过程)
时,求n的值.(直接写出结果,不必写出解答过程)
【答案】
(1)
解:∵AD∥BC,
∴∠EFO=∠BGO,
∵FG为BE的垂直平分线,
∴BO=OE;
∵在△EFO和△BGO中, 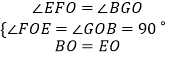 ,
,
∴△EFO≌△BGO,
∴FO=GO
∵EO=BO,且BE⊥FG
∴四边形BGEF为菱形.
(2)
解:当AB=a,n=3时,AD=2a,AE= ![]() ,
,
根据勾股定理可以计算BE= ![]() ,
,
∵AF=AE﹣EF=AE﹣BF,在Rt△ABF中AB2+AF2=BF2,计算可得AF= ![]() ,EF=
,EF= ![]() ,
,
∵菱形BGEF面积= ![]() BEFG=EFAB,计算可得FG=
BEFG=EFAB,计算可得FG= ![]()
(3)
解:设AB=x,则DE= ![]() ,
,
S1=BGAB,S2=BCAB
当 ![]() =
= ![]() 时,
时, ![]() =
= ![]() ,可得BG=
,可得BG= ![]() ,
,
在Rt△ABF中AB2+AF2=BF2,计算可得AF= ![]() ,
,
∴AE=AF+FE=AF+BG= ![]() ,DE=AD﹣AE=
,DE=AD﹣AE= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴n=6.
【解析】(1)先求证△EFO≌△BGO,可得FO=GO,再根据对角线互相垂直且平分的四边形是菱形,即可证明四边形BFEG为菱形;(2)根据菱形面积不同的计算公式(底乘高和对角线乘积的一半两种计算方式)可计算FG的长度;(3)根据菱形面积底乘高的计算方式可以求出BG长度,根据勾股定理可求出AF的长度,即可求出ED的长度,即可计算n的值.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 . 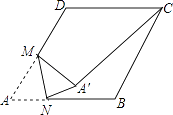
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E.F分别在AB、CD上,AE=CF,连接AF,BF,DE,CE,分别交于H、G.
求证:(1)四边形AECF是平行四边形。(2)EF与GH互相平分。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(1,0)和点(0,﹣2),且顶点在第三象限,设P=a﹣b+c,则P的取值范围是( ) 
A.﹣4<P<0
B.﹣4<P<﹣2
C.﹣2<P<0
D.﹣1<P<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知射线 DM与直线AB交于点A,线段EC与直线AB交于点C,AB∥DE.
(1)当∠MAC=100°,∠BCE=120°时,把EC绕点E旋转多大角度(所求角度小于180°)时,可判定MD∥EC?请你设计出两种方案,并画出草图;
(2)若将EC绕点E逆时针旋转60°时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在△ABC和△ADE中,AB=AC=AD=AE,当∠BAC+∠DAE=180° 时,我们称△ABC与△DAE互为“顶补等腰三角形”,△ABC的边BC上的高线AM叫做△ADE的“顶心距”,点A叫做“旋补中心”.

(1)特例感知:在图2,图3中,△ABC与△DAE互为“顶补等腰三角形”,AM是“顶心距”。
①如图2,当∠BAC=90°时,AM与DE之间的数量关系为AM= DE;
②如图3,当∠BAC=120°,ED=6时,AM的长为 。
(2)猜想论证:
在图1中,当∠BAC为任意角时,猜想AM与DE之间的数量关系,并给予证明。

(3)拓展应用
如图4,在四边形ABCD中,AD=AB,CD=BC,∠B=90°,∠A=60°,CA=![]() ,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
,在四边ABCD的内部找到点P,使得△PAD与△PBC互为“顶补等腰三角形”。并回答下列问题。
①请在图中标出点P的位置,并描述出该点的位置为 ;
②直接写出△PBC的“顶心距”的长为 。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车从A地驶往B地,前三分之一路段为普通公路,其余路段为高速公路.已知汽车在普通公路上行驶的速度为60km/h,在高速公路上行驶的速度为100km/h.汽车从A地到B地共行驶了2.2h.请你根据以上信息,就该汽车行驶的“路程”或“时间”,提出一个问题: ,并列出方程,求出解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com