
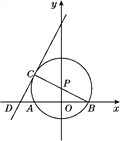
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
【答案】(1)C(-2,2);(2)证明见解析.
【解析】试题分析:
(1)Rt△OBP中,由勾股定理得到OP的长,连接AC,因为BC是直径,所以∠BAC=90°,因为OP是△ABC的中位线,所以OA=2,AC=2,即可求解;
(2)由点C的坐标可得直线CD的解析式,则可求点D的坐标,从而可用SAS证△DAC≌△POB,进而证∠ACB=90°.
试题解析:
(1)解:如图,连接CA.∵OP⊥AB,∴OB=OA=2.∵OP2+BO2=BP2,
∴OP2=5-4=1,OP=1.∵BC是⊙P的直径,∴∠CAB=90°.
∵CP=BP,OB=OA,∴AC=2OP=2.∴B(2,0),P(0,1),C(-2,2).
(2)证明:∵直线y=2x+b过C点,∴b=6.∴y=2x+6.
∵当y=0时,x=-3,∴D(-3,0).∴AD=1.∵OB=AC=2,AD=OP=1,
∠CAD=∠POB=90°,∴△DAC≌△POB.∴∠DCA=∠ABC.
∵∠ACB+∠CBA=90°,∴∠DCA+∠ACB=90°,即CD⊥BC.∴CD是⊙P的切线.


科目:初中数学 来源: 题型:
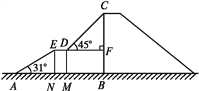
【题目】下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,已知以△ABC的边AB、AC分别向外作等腰直角△ABD与等腰直角△ACE,∠BAD=∠CAE=90°,连接BE和CD相交于点O,AB交CD于点F,AC交BE于点G,求证:BE=DC,且BE⊥DC.
(2)探究:若以△ABC的边AB、AC分别向外作等边△ABD与等边△ACE,连接BE和CD相交于点O,AB交CD于点F,AC交BE于G,如图2,则BE与DC还相等吗?若相等,请证明,若不相等,说明理由;并请求出∠BOD的度数?

查看答案和解析>>
科目:初中数学 来源: 题型:
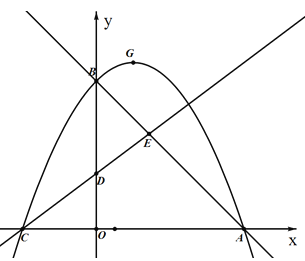
【题目】如图,在平面直角坐标系中,抛物线试纸y=ax2+bx+c与x轴交于点A,C,与y轴交于点B.已知点A坐标为(8,0),点B为(0,8),点D为(0,3),tan∠DCO=![]() ,直线AB和直线CD相交于点E.
,直线AB和直线CD相交于点E.
⑴ 求抛物线的解析式,并化成y=a(x-m)2+h的形式;
⑵ 设抛物线的顶点为G,请在直线AB上方的抛物线上求点P的坐标,使得S△ABP=S△ABG.
⑶ 点M为直线AB上的一点,过点M作x轴的平行线分别交直线AB,CD于点M,N,连结DM,DN,是否存在点M,使得△DMN为等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
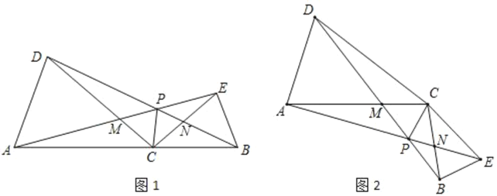
【题目】如图1,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD=∠BCE=30°,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.
(1)线段AE与DB的数量关系为 ;请直接写出∠APD= ;
(2)将△BCE绕点C旋转到如图2所示的位置,其他条件不变,探究线段AE与DB的数量关系,并说明理由;求出此时∠APD的度数;
(3)在(2)的条件下求证:∠APC=∠BPC.
查看答案和解析>>
科目:初中数学 来源: 题型:
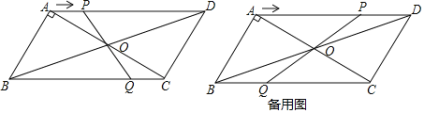
【题目】如图,在□ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)当t=3时四边形OQCD的面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
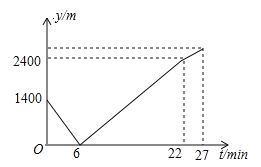
【题目】(2017湖北省鄂州市,第8题,3分)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,图中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
①打电话时,小东和妈妈的距离为1400米;
②小东和妈妈相遇后,妈妈回家的速度为50m/min;
③小东打完电话后,经过27min到达学校;
④小东家离学校的距离为2900m.
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
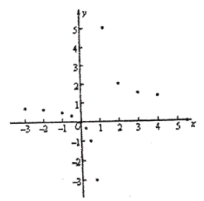
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com