
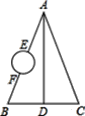
【题目】如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是
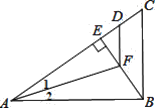
A. BF=DF B. ∠1=∠EFD C. BF>EF D. FD∥BC
【答案】B
【解析】
根据余角的性质得到∠C=∠ABE,∠EBC=∠BAC.根据SAS推出△ABF≌△ADF,根据全等三角形的性质得到BF=DF,故A正确;由全等三角形的性质得到∠ABE=∠ADF,等量代换得到∠ADF=∠C,根据平行线的判定得到DF∥BC,故D正确;根据直角三角形的性质得到DF>EF,等量代换得到BF>EF;故C正确;根据平行线的性质得到∠EFD=∠EBC=∠BAC=2∠1,故B错误.
∵AB⊥BC,BE⊥AC,∴∠C+∠BAC=∠ABE+∠BAC=90°,∴∠C=∠ABE.同理:∠EBC=∠BAC.
在△ABF与△ADF中,∵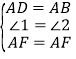 ,∴△ABF≌△ADF,∴BF=DF,故A正确,
,∴△ABF≌△ADF,∴BF=DF,故A正确,
∵△ABF≌△ADF,∴∠ABE=∠ADF,∴∠ADF=∠C,∴DF∥BC,故D正确;
∵∠FED=90°,∴DF>EF,∴BF>EF;故C正确;
∵DF∥BC,∴∠EFD=∠EBC.∵∠EBC=∠BAC=∠BAC=2∠1,∴∠EFD=2∠1,故B错误.
故选B.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(11分)阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集到20株西红柿秧上小西红柿的个数:32 39 45 55 60 54 60 28 56 41 51 36 44 46 40 53 37 47 45 46
(1)前10株西红柿秧上小西红柿个数的平均数是 ,中位数是 ,众数是 ;
(2)若对这20个数按组距8进行分组,请补全频数分布表及频数分布直方图:
个数分组 | 28≤x<36 | 36≤x<44 | 44≤x<52 | 52≤x<60 | 60≤x<68 |
频数 | 2 | 2 |
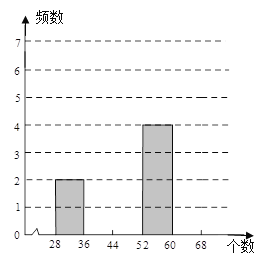
(3)通过频数分布直方图试分析此大棚中西红柿的长势。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线相交于点O,点M,N分别是边BC,CD上的动点(不与点B,C,D重合),AM,AN分别交BD于点E,F,且∠MAN始终保持45°不变.
(1)求证: ![]() =
= ![]() ;
;
(2)求证:AF⊥FM;
(3)请探索:在∠MAN的旋转过程中,当∠BAM等于多少度时,∠FMN=∠BAM?写出你的探索结论,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.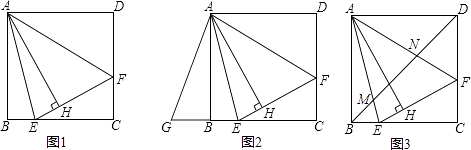
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示.A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄AC,AD间也有公路相连,且公路AD是南北走向,AC=3km,只有AB之间由于间隔了一个小湖,所以无直接相连的公路.现决定在湖面上造一座斜拉桥,测得AE=1.2km,BF=0.7km.试求建造的斜拉桥长至少有多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF= ![]() .
. 
(1)求证:四边形ABDE是平行四边形;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,以CD为边作等边三角形CDE,BE与AC相交于点M,则∠AMD的度数是( )
A.75°
B.60°
C.54°
D.67.5°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com