
 如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C作直线DE∥AB交圆于D,E两点,BD与OC交于点F,则∠BDE=15°.
如图,在⊙O中,AB为直径,Rt△OBC的直角边OC=BC=1,过点C作直线DE∥AB交圆于D,E两点,BD与OC交于点F,则∠BDE=15°. 分析 过点O作OG⊥DE于点G,过点C作CH⊥AB于点H,根据等腰三角形的性质求出OG和OD的长度,然后即可求出∠ODG的度数,从而求出答案.
解答 解: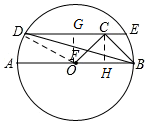 过点O作OG⊥DE于点G,过点C作CH⊥AB于点H,
过点O作OG⊥DE于点G,过点C作CH⊥AB于点H,
∵△OCB是等腰直角三角形,OC=BC=1,
∴由勾股定理可知:OB=$\sqrt{2}$,
∴OD=OB=$\sqrt{2}$,
∴CH=OH=OG=$\frac{\sqrt{2}}{2}$,
∴OD=2OG,
∴∠ODG=30°,
∵DE∥AB,
∴∠ODG=∠DOA=30°,
∴∠ODB=$\frac{1}{2}$∠DOA=15°,
∴∠BDE=∠ODG-∠ODB=15°
故答案为:15°
点评 本题考查圆的综合问题,涉及含30°的直角三角形的性质,等腰直角三角形的性质,垂径定理、勾股定理,矩形的性质等知识,综合程度较高.


科目:初中数学 来源: 题型:填空题
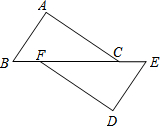 如图,AB=DE,∠A=∠D=90°,那么要得到△ABC≌△DEF,可以添加一个条件是AC=DF,△ABC与△DEF全等的理由是SAS.
如图,AB=DE,∠A=∠D=90°,那么要得到△ABC≌△DEF,可以添加一个条件是AC=DF,△ABC与△DEF全等的理由是SAS.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
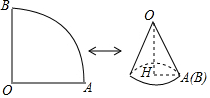 如图,已知扇形AOB的圆心角为90°,面积为16π.
如图,已知扇形AOB的圆心角为90°,面积为16π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:| 组别 | 课堂发言次数n |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
在某市第四次党代会上,提出了建设美丽城市决胜全面小康的奋斗目标,为策应市委号召,学校决定改造校园内的一小广场,如图是该广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com