
【题目】如图,在等腰△ABC中,BA=BC,∠ABC=100°,AB平分∠WAC.在线段AC上有一动点D,连接BD并作∠DBE,使∠DBE=50°,BE边交直线AW于点E,连接DE.
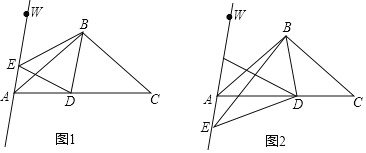
(1)如图1,当点E在射线AW上时,直接判断:AE+DE CD;(填“>”、“=”或“<”)
(2)如图2,当点E在射线AW的反向延长线上时,
①判断线段CD,DE,AE之间的数量关系,并证明;
②若S四边形ABDE﹣S△BCD=6,且2DE=5AE,AD=![]() AE,求S△ABC的值.
AE,求S△ABC的值.
【答案】(1)=;(2)①DE=CD+AE.理由见解析;②S△ABC=![]() .
.
【解析】
(1)在AC上取一点T,使得∠TBD=![]() ∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
(2)①在AC的延长线上取一点T,使得∠TBD=![]() ∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
∠ABC,连接BT,利用ASA即可证出△BAE≌△BCT,从而得出:TC=AE,BE=BT,再利用SAS即可证出△DBE≌△DBT,从而证出DE=DT,即可得出结论;
②根据全等三角形的性质可得:S△ABE=S△BCT,S△BDE=S△BDT,然后根据已知条件可得S△BCT=3,设DE=5k,AE=2k,然后利用k求出AC:CT,最后根据同高时,三角形的面积之比等于底之比即可求出S△ABC的值.
解:(1)如图1中,在AC上取一点T,使得∠TBD=![]() ∠ABC,连接BT.
∠ABC,连接BT.
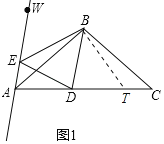
∵∠TBD=![]() ∠ABC,∠DBE=50°=
∠ABC,∠DBE=50°=![]() ∠ABC,
∠ABC,
∴∠CBT+∠ABD=∠ABD+∠ABE=![]() ∠ABC,
∠ABC,
∴∠ABE=∠CBT,
∵BA=BC,
∴∠BAC=∠C,
∵∠BAE=∠BAC,
∴∠EAB=∠C,
在△BAE和△BCT中
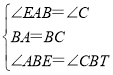
∴△BAE≌△BCT(ASA),
∴TC=AE,BE=BT,
在△DBE和△DBT中

∴△DBE≌△DBT(SAS),
∴DE=DT,
∴AE+DE=CT+DT=CD.
故答案为=.
(2)①结论:DE=CD+AE.
理由:如图2中,在AC的延长线上取一点T,使得∠TBD=![]() ∠ABC,连接BT.
∠ABC,连接BT.
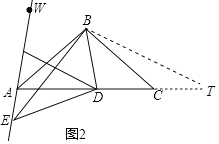
∵∠TBD=![]() ∠ABC,∠DBE=50°=
∠ABC,∠DBE=50°=![]() ∠ABC,
∠ABC,
∴∠CBT+∠CBD=∠CBD+∠ABE=![]() ∠ABC,
∠ABC,
∴∠ABE=∠CBT,
∵BA=BC,
∴∠BAC=∠ACB,
∵∠BAE=∠BAC,
∴∠WAB=∠ACB,
∴∠BAE=∠BCT,
在△BAE和△BCT中
∴△BAE≌△BCT(ASA),
∴TC=AE,BE=BT,
在△DBE和△DBT中

∴△DBE≌△DBT(SAS),
∴DE=DT,
∴DE=DC+CT=AE+CD.
②由①可知:S△ABE=S△BCT,S△BDE=S△BDT,
∵S四边形ABDE﹣S△BCD=6,
∴S△BDC+2S△BCT﹣S△BDC=6,
∴S△BCT=3,
∵2DE=5AE,AD=![]() AE,设DE=5k,AE=2k,则AD=
AE,设DE=5k,AE=2k,则AD=![]() k,CD=DT﹣CT=DE﹣AE=3k,
k,CD=DT﹣CT=DE﹣AE=3k,
∴AC=AD+CD=![]() k+3k=
k+3k=![]() k,
k,
∴AC:CT=67:18,
∴S△ABC=![]() ×S△CBT=
×S△CBT=![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)2m2-4m+1-2(m2+2m-![]() ),其中m=-1;
),其中m=-1;
(2)5xy2-[2x2y-(2x2y-3xy2)],其中(x-2)2+|y+1|=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】梅里雪山,是位于西藏察隅县东部与云南迪庆藏族自治州德钦县境云岭乡西部的一座南北走向的庞大的雪山群,全长有150公里.它在藏区称卡瓦格博雪山,“梅里”一词为德钦藏语mainri汉译,意思是药山,因盛产各种名贵药材而得名.同时它也是雍仲苯教圣地,和西藏的冈仁波齐、青海的阿尼玛卿山、青海的尕朵觉沃并称为藏传佛教四大神山.最高峰卡瓦格博峰海拔高度为6740米,是云南省最高的山峰.用科学记数法表示6740米应为( )米.
A.674×10B.67.4×![]() C.6.74
C.6.74![]() D.0.674
D.0.674![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ABC=45°.点D在AB上,点E在BC上,且AE⊥CD,若AE=CD,BE:CE=5:6,S△BDE=75,则S△ABC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年9月1日,长春首届航空开放日在长春大房身机场正式举行,空军八一飞行表演队的新换装歼-10飞机,进行了精彩的特技飞行表演,其中一架飞机起飞0.5千米后的高度变化如下表:
高度变化 | 上升4.2 | 下降3.5 | 上升1.4 | 下降1.2 |
记作 | +4.2 | -3.5 | +1.4 | -1.2 |
(1)此时这架飞机飞离地面的高度是多少千米?
(2)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.6干米,下降2.8千米,再上升1.5千米,最后下降0.9千米.若飞机平均上升1干米需消耗6升燃油,平均下降1千米需消耗4升燃油,那么这架飞机在这4个特技表演过程中,一共消耗了多少升燃油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按以下步骤作图:①分别以B、C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为( )
BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD.若∠B=30°,∠A=55°,则∠ACD的度数为( )

A. 65°B. 60°C. 55°D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
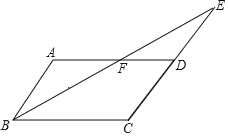
【题目】如图,已知平行四边形ABCD中,∠ABC的平分线与边CD的延长线交于点E,与AD交于点F,且AF=DF,
①求证:AB=DE;
②若AB=3,BF=5,求△BCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某服装厂现有甲种布料50米,乙种布料27米,现计划用这两种布料生产A,B两种型号的时装共60套. 已知做一套A型号的时装需用甲种布料1米,乙种布料0.2米,可获利30元;做一套B型号的时装需用甲种布料0.5米,乙种布料0.8米,可获利20元. 设生产A型号的时装套数为x,用这批布料生产两种型号的时装所获得的总利润为y元.
(1)求y(元)与x(套)之间的函数表达式,并求出自变量的取值范围.
(2)当生产A型号的时装多少套时,能使该厂所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com