练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】四边形ABCD中，∠A＝∠B＝∠C＝90°，请你再添加一个条件，使该四边形是正方形，你添加的条件是__________．（填写其中一种情况即可）

    【答案】答案不唯一，如AB=BC

    【解析】

    先由∠A=∠B=∠C=90°，得出四边形ABCD是矩形，再根据正方形的判定：有一组邻边相等的矩形是正方形可得出结果．

    ∵∠A=∠B=∠C=90°，∴四边形ABCD是矩形．

    又∵有一组邻边相等的矩形是正方形，∴可填：AB=BC．

    故答案为：AB=BC．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图（1），E是直线AB、CD内部一点，AB∥CD，连接EA、ED．

    （1）探究：

    ①若∠A=30°，∠D=40°，则∠AED等于多少度？

    ②若∠A=20°，∠D=60°，则∠AED等于多少度？

    ③在图（1）中∠AED、∠EAB、∠EDC有什么数量关系，并证明你的结论．

    （2）拓展：如图（2），射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的四个区域（不含边界，其中③④位于直线AB的上方），P是位于以上四个区域上点，猜想：∠PEB、∠PFC、∠EPF之间的关系．（不要求证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，分别以AB、AD为边向外作等边△ABE，△ADF，延长CB交AE于点G，点G落在点A、E之间，连接EF、CF．则以下四个结论：①CG⊥AE；②△CDF≌△EBC；③∠CDF =∠EAF；④△ECF是等边三角形．其中一定正确的是 ．（把正确结论的序号都填上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=﹣x2不具有的性质是（ ）
    A.开口向上
    B.对称轴是y轴
    C.在对称轴的左侧，y随x的增大而增大
    D.最高点是原点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】⊙O为△ABC的外接圆，过圆外一点P作⊙O的切线PA，且PA∥BC．

    （1）如图1，求证：△ABC为等腰三角形：

    （2）如图2，在AB边上取一点E，AC边上取一点F，直线EF交PA于点M，交BC的延长线于点N，若ME=FN，求证：AE=CF；

    （3）如图3，在（2）的条件下，连接OE、OF，∠EOF=120°，，EF=，求⊙O的半径长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=﹣x+3交y轴于点A，交x轴与点B，抛物线y=﹣x2+bx+c经过点A和点B，点P为抛物线上直线AB上方部分上的一点，且点P的横坐标为t，过P作PE∥x轴交直线AB于，作PH⊥x轴于H，PH交直线AB于点F．

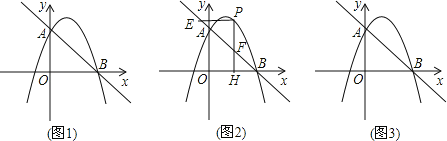
    （1）求抛物线解析式；

    （2）若PE的长为m，求m关于t的函数关系式；

    （3）是否存在这样的t值，使得∠FOH﹣∠BEH=45°？若存在，求出t值，并求tan∠BEH的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】过点P（2，﹣3）且垂直于y轴的直线交y轴于点Q，那么Q点的坐标为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在某建筑物AC上挂着宣传条幅BC，小明站在点F处，看条幅顶端B，测得仰角为30°，再往条幅方向前行40米到达点E处，看到条幅顶端B，测得仰角为60°．

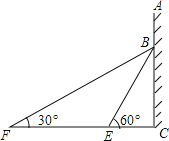
    （1）求宣传条幅BC的长（小明的身高不计，结果保留根号）；

    （2）若小明从点F到点E用了80秒钟，按照这个速度，小明从点F到点C所用的时间为多少秒？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列运算中正确的是（ ）

    A．a2a3=a5 B．（a2）3=a5 C．a6÷a2=a3 D．a5+a5=2a10

    查看答案和解析>>

    同步练习册答案