
|
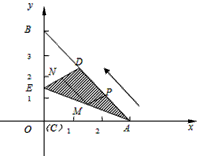
解:(1) 据题意,△AOE≌△ADE, |
 |
| (2)∵PM∥DE,MN∥AD,且∠ADE=90°, ∴四边形PMND是矩形, ∵AP=t×1=t, ∴PD=3-t, ∵△AMP∽△AED, ∴ 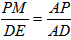 , ,∴PM=  , ,∴  , ,∴  或 或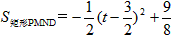 , ,当  时, 时,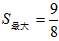 ; ; |
|
| (3)△ADM为等腰三角形有以下二种情况: ①当MD=MA时,点P是AD中点, ∴ 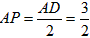 , ,∴  (秒), (秒),∴当 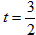 时,A、D、M三点构成等腰三角形, 时,A、D、M三点构成等腰三角形,过点M作MF⊥OA于F, ∵△APM≌△AFM, ∴AF=AP=  ,MF=MP= ,MF=MP=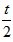 = = , ,∴OF=OA-AF=3- 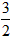 = =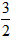 , ,∴M( 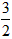 , ,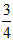 ); );②当AD=AM=3时, △AMP∽△AED, ∴  , ,∴ 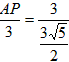 , ,∴ 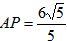 , ,∴ 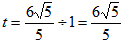 (秒), (秒),∴当 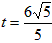 秒时,A、D、M三点构成等腰三角形, 秒时,A、D、M三点构成等腰三角形,过点M作MF⊥OA于F ∵△AMF≌△AMP, ∴AF=AP= 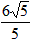 ,FM=PM= ,FM=PM=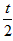 = =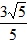 , ,∴OF=OA-AF=3-  , ,∴M(3- 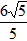 , ,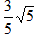 )。 )。 |
  |


科目:初中数学 来源: 题型:
 如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.
如图所示,Rt△ABC中,已知∠BAC=90°,AB=AC=2,点D在BC上运动(不能到达点B,C),过点D作∠ADE=45°,DE交AC于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com