
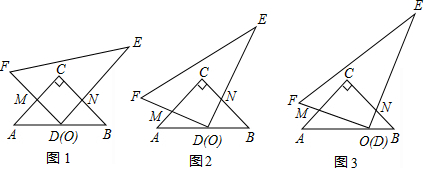
分析 (1)连接OC,证△COM≌△CON,得出对应边相等即可;
(2)连接OC,证△AOM≌△CON即可,得出对应边相等;
(3)证明四边形OMCN是矩形,得出ON=MC,再证明△AOM是等腰直角三角形,得出OM=AM,即可得出结论.
解答 解: (1)OM=ON;理由如下:连接OC.
(1)OM=ON;理由如下:连接OC.
∵AC=BC,O是AB中点,∠ACB=90°,
∴OA=OB,CO⊥AB,∠ACO=∠BCO=45°,
∵DF⊥AC于M,DE⊥BC于N,
∴∠OMC=∠ONC=90°,
在△COM和△CON中,$\left\{\begin{array}{l}{∠OMC=∠ONC}&{\;}\\{∠ACO=∠BCO}&{\;}\\{OC=OC}&{\;}\end{array}\right.$,
∴△COM≌△CON(AAS),
∴OM=ON;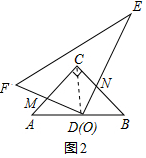
(2)存在;理由如下:连接OC,
∵AC=BC,O是AB中点,∠ACB=90°,
∴∠A=∠B=45°,OA=OB,CO⊥AB,∠ACO=∠BCO=45°,OC=$\frac{1}{2}$AB=OA,
∴∠A=∠OCN,
∵∠EOF=90°,
∴∠AOM=∠CON,
在△AOM和△CON中,$\left\{\begin{array}{l}{∠A=∠OCN}&{\;}\\{∠AOM=∠CON}&{\;}\\{OA=CO}&{\;}\end{array}\right.$,
∴△AOM≌△CON(AAS),
∴OM=ON;
(3)OM+ON=AC,理由如下:
∵∠ACB=∠FDE=90°,DF⊥AC于M,DE⊥BC于N,
∴四边形OMCN是矩形,
∴ON=MC,
又∵∠A=45°,
∴△AOM是等腰直角三角形,
∴OM=AM,
∴OM+ON=AM+MC=AC.
点评 本题是三角形综合题目,考查了全等三角形的性质和判定,等腰直角三角形的性质与判定,直角三角形斜边上中线性质等知识点的综合运用,题目综合性比较强,有一定的难度,证明三角形全等是解决问题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题
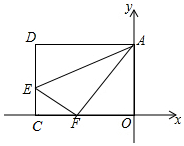 如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(-10,8),则△AEF的面积为( )
如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(-10,8),则△AEF的面积为( )| A. | 15 | B. | 20 | C. | 25 | D. | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )| A. | (1,0) | B. | (-1,0) | C. | (-1,1) | D. | (1,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com