
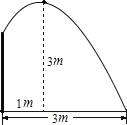
【题目】要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点![]() 和点
和点![]() ,给出如下定义:若
,给出如下定义:若![]() ,则称点
,则称点![]() 为点
为点![]() 的限变点.例如:点
的限变点.例如:点![]() 的限变点的坐标是
的限变点的坐标是![]() ,点
,点![]() 的限变点的坐标是
的限变点的坐标是![]() .
.
(1)①点![]() 的限变点的坐标是___________;
的限变点的坐标是___________;
②在点![]() ,
,![]() 中有一个点是函数
中有一个点是函数![]() 图象上某一个点的限变点,这个点是_______________;
图象上某一个点的限变点,这个点是_______________;
(2)若点![]() 在函数
在函数![]() 的图象上,其限变点
的图象上,其限变点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若点![]() 在关于
在关于![]() 的二次函数
的二次函数![]() 的图象上,其限变点
的图象上,其限变点![]() 的纵坐标
的纵坐标![]() 的取值范围是
的取值范围是![]() 或
或![]() ,其中
,其中![]() .令
.令![]() ,求
,求![]() 关于
关于![]() 的函数解析式及
的函数解析式及![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边![]() 中,点
中,点![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,则下列结论中:①
,则下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论的个数是( )
,其中正确的结论的个数是( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形![]() ,
,![]()
(1)如图1,当点![]() 分别在边
分别在边![]() ,
,![]() 上,连接
上,连接![]() ,求证:
,求证:![]()
(2)如图2,点![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,当点
,当点![]() 分别在
分别在![]() ,
,![]() 上,连接
上,连接![]() ,请探究线段
,请探究线段![]() ,
,![]() ,
,![]() 之间满足的数量关系,并加以证明.
之间满足的数量关系,并加以证明.
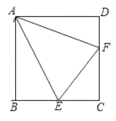
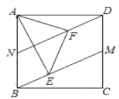
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格上有A、B、O三点,如果用(3,3)表示方格纸上A点的位置,(1,1)表示B点的位置,O点也在网格点上.
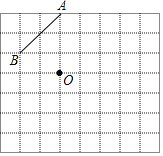
(1)作出点B关于直线OA的轴对称点C,写出点C坐标.(不写作法,但要在图中标出字母);
(2)作出△ABC关于点O的中心对称图形△A′B′C′,写出A′、B′、C′三点的坐标;(不写作法,但要标出字母);
(3)若网格上的最小正方形边长为1,求出△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
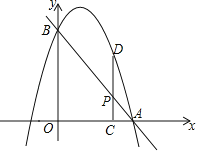
【题目】如图,已知直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC
轴于点A、B,抛物线过A,B两点,点P是线段AB上一动点,过点P作PC![]()
![]() 轴于点C,交抛物线于点D.
轴于点C,交抛物线于点D.
(1)若抛物线的解析式为![]() ,设其顶点为M,其对称轴交AB于点N.
,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为1时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形与![]() AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
AOB相似?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块等腰三角形白铁皮余料ABC,它的腰AB=10cm,底边BC=12cm.
(1)圆圆同学想从中裁出最大的圆,请帮他求出该圆的半径;
(2)方方同学想从中裁出最大的正方形,请帮他求出该正方形的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com