
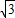 ,求直线PD的函数关系式;
,求直线PD的函数关系式;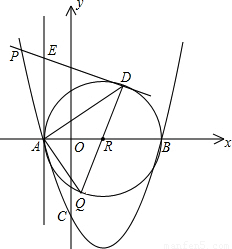
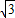 ,即可求出EA的长,也就得到了E点的坐标;在Rt△EAR中,根据EA、AR的值,即可求出∠ERA的度数,进而可求出∠DRF的度,从而在Rt△DRF中,通过解直角三角形求出RF、DF的长,由此求得D点坐标,用待定系数法即可求出直线DP的解析式;(需注意的是AE的长为正值,但是E点的纵坐标有正负两种情况,所以要分类讨论)
,即可求出EA的长,也就得到了E点的坐标;在Rt△EAR中,根据EA、AR的值,即可求出∠ERA的度数,进而可求出∠DRF的度,从而在Rt△DRF中,通过解直角三角形求出RF、DF的长,由此求得D点坐标,用待定系数法即可求出直线DP的解析式;(需注意的是AE的长为正值,但是E点的纵坐标有正负两种情况,所以要分类讨论)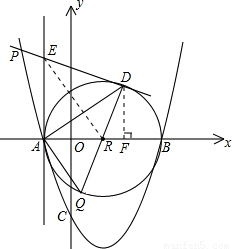 解:(1)∵抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,
解:(1)∵抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,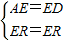 ,
,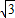 ,
,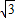 ,
, AR•AE=2
AR•AE=2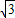 ,
,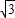 ,
,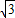 )或E2(-1,-2
)或E2(-1,-2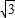 ),
),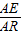 =
=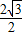 =
=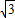 ,
,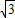 ,
,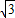 ),
),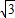 ),D(2,
),D(2,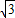 )的坐标代入得,
)的坐标代入得,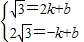 ,
,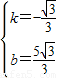 ,
,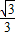 x+
x+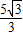 ,
,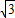 ),
),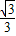 x-
x-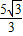 ,
,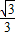 x+
x+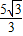 或y=
或y=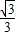 x-
x-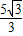 ;
;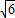 ;
;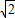 ,
,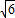 ,2)、P2(1-
,2)、P2(1-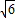 ,2)、P3(1+
,2)、P3(1+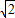 ,-2)、P4(1-
,-2)、P4(1-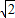 ,-2).
,-2).

科目:初中数学 来源: 题型:
 =-1,与x轴交于点C,且∠ABC=90°
=-1,与x轴交于点C,且∠ABC=90°查看答案和解析>>
科目:初中数学 来源: 题型:
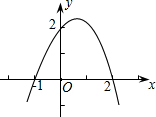 如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )
如图,抛物线与两坐标轴的交点分别为(-1,0),(2,0),(0,2),则当y>2时,自变量x的取值范围是( )A、0<x<
| ||
| B、0<x<1 | ||
C、
| ||
| D、-1<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
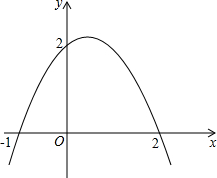 (2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),
(2012•翔安区模拟)如图,抛物线与两坐标轴的交点坐标分别为(-1,0),(2,0),(0,2),| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,以AB为直径作圆R,过抛物线上一点P作直线PD切圆R于D,并与圆R的切线AE交于点E,连接DR并延长交圆R于点Q,连接AQ,AD.
如图,抛物线与坐标轴分别交于点A(a,0),B(b,0),C(0,c),其中abc=9,a、b、c均为整数,且a<0,b>0,c<0,|a|<|b|=|c|,以AB为直径作圆R,过抛物线上一点P作直线PD切圆R于D,并与圆R的切线AE交于点E,连接DR并延长交圆R于点Q,连接AQ,AD.| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com