
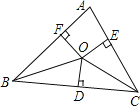
【题目】如图,O是△ABC内一点,且O到三边AB、BC、CA的距离OF=OD=OE,若∠BAC=70°,∠BOC= .
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A. a:b:c=4:5:6 B. b 2=a 2-c2 C. ∠A=∠C-∠B D. a=3,b=4,c=5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简,求值
(1)5x2y+{xy﹣[5x2y﹣(7xy2+![]() xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣
xy)]﹣(4x2y+xy)}﹣7xy2,其中x=﹣![]() ,y=﹣16.
,y=﹣16.
(2)A=4x2﹣2xy+4y2,B=3x2﹣6xy+3y2,且|x|=3,y2=16,|x+y|=1,求4A+[(2A﹣B)﹣3(A+B)]的值.
(3)如果m﹣3n+4=0,求:(m﹣3n)2+7m3﹣3(2m3n﹣m2n﹣1)+3(m3+2m3n﹣m2n+n)﹣m﹣10m3的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:在平面直角坐标系中,以点M(0,![]() )为圆心,2
)为圆心,2![]() 为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.
为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于点P,连接PC交x轴于点E.

(1)求点C,P的坐标;
(2)求弓形![]() 的面积;
的面积;
(3)探求线段BE和OE存在何种数量关系,并证明你所得到的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.
小明发现,利用轴对称做一个变化,在BC上截取CA′=CA,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).
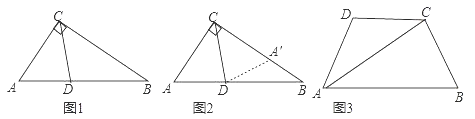
请回答:
(1)在图2中,小明得到的全等三角形是△ ≌△ ;
(2)BC和AC、AD之间的数量关系是 .
参考小明思考问题的方法,解决问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9.求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)如图,奥运福娃在5×5的方格(每小格边长为1m)上沿着网格线运动.贝贝从A处出发去寻找B、C、D处的其它福娃,规定:向上向右走为正,向下向左走为负。如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(-1,-4),其中第一个数表示左右方向,第二个数表示上下方向,那么图中
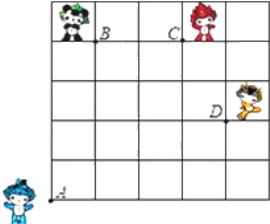
(1)A→C( , );B→C( , );C→ (-3,-4);
(2)若贝贝的行走路线为A→B→C→D,请计算贝贝走过的路程;
(3)若贝贝从A处去寻找妮妮的行走路线依次为(+2,+2),(+2,-1),(-2,+3),(-2,-2),请在图中标出妮妮的位置E点.
(4)在(3)中贝贝若每走1m需消耗1.5焦耳的能量,则贝贝寻找妮妮过程中共需消耗多少焦耳的能量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一架2.5米长的梯子,斜靠在一竖直的墙上,这时梯足到墙底端的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯足将向外移多少米?(5分)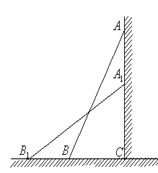
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 李老师做了个长方形教具,其中一边长为2a+b,另一边长为a﹣b,则该长方形周长为( )
A. 6a+b B. 6a C. 3a D. 10a﹣b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com