
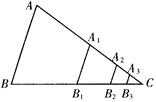
如图,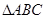 的面积为1,分别取AC、BC两边中点A1、B1,四边形A1ABB1的面积为____________,再分别取A1C、B1C的中点A2、B2;又再取A2C、B2C的中点A3、B3;依次取下去……,利用这一图形能直观地计算出
的面积为1,分别取AC、BC两边中点A1、B1,四边形A1ABB1的面积为____________,再分别取A1C、B1C的中点A2、B2;又再取A2C、B2C的中点A3、B3;依次取下去……,利用这一图形能直观地计算出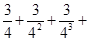 ……
……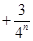 = .
= . 
 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏泰兴市实验中学八年级上学期期末考试数学试卷(带解析) 题型:解答题
探究
如图①,在□ABCD的形外分别作等腰直角△ABF和等腰直角△ADE,∠FAB=∠EAD=90°,连结AC、EF.在图中找一个与△FAE全等的三角形,并说明理由.(5分)
应用以□ABCD的四条边为边,在其形外分别作正方形,如图②,连结EF、GH、IJ、KL.若图中阴影部分四个三角形的面积和为12,则□ABCD的面积为 .(3分)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江宁波城区五校联考初三第一学期12月月考数学试卷(解析版) 题型:填空题
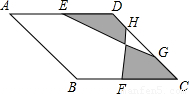
如图,在面积为24的菱形ABCD中,E、F分别是边AD、BC的中点,点G、H在DC边上,且GH =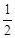 DC.则图中阴影部分面积为 .
DC.则图中阴影部分面积为 .
查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆巴南区全善学校(先华中学)九年级第三次月考数学试卷(解析版) 题型:填空题
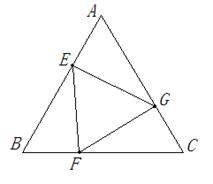
如图正三角形 边长为2,
边长为2, 分别是
分别是 上的点,且
上的点,且 ,设
,设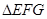 的面积为
的面积为 ,
,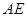 的长为
的长为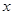 ,则
,则 的最小值为_____________。
的最小值为_____________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com