
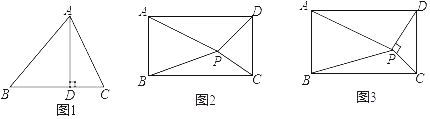
【题目】(几何背景)如图1,AD为锐角△ABC的高,垂足为D.求证:AB2﹣AC2=BD2﹣CD2
(知识迁移)如图2,矩形ABCD内任意一点P,连接PA、PB、PC、PD,请写出PA、PB、PC、PD之间的数量关系,并说明理由.
(拓展应用)如图3,矩形ABCD内一点P,PC⊥PD,若PA=a,PB=b,AB=c,且a、b、c满足a2﹣b2=![]() c2,则
c2,则![]() 的值为 (请直接写出结果)
的值为 (请直接写出结果)
【答案】【几何背景】:详见解析;【知识迁移】:详见解析;【拓展应用】:![]()
【解析】
几何背景:由 Rt△ABD中,AD2=AB2﹣BD2,Rt△ACD中,AD2=AC2﹣CD2,则结论可证.
知识迁移:过P点作PE⊥AD,延长EP交BC于F,可证四边形ABFE,四边形DCFE是矩形.根据上面的结论求得PA、PB、PC、PD之间的数量关系.
拓展应用:根据勾股定理可列方程组,可求PD=![]() c,PC=
c,PC=![]() c即可得
c即可得![]() .
.
解:几何背景:在Rt△ABD中,AD2=AB2﹣BD2
Rt△ACD中,AD2=AC2﹣CD2,
∴AB2﹣BD2=AC2﹣CD2,
∴AB2﹣AC2=BD2﹣CD2.
知识迁移:BP2﹣PC2 =BF2﹣CF2.
如 图:
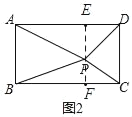
过P点作PE⊥AD,延长EP交BC于F
∴四边形ABCD是矩形
∴AD∥BC∠BAD=∠ADC=∠DCB=∠ABC=90°
又∵PE⊥AD
∴PF⊥BC
∵PE是△APD的高
∴PA2﹣PD2=AE2﹣DE2.
∵PF是△PBC的高
∴BP2﹣PC2 =BF2﹣CF2.
∵∠BAD=∠ADC=∠DCB=∠ABC=90°,PE⊥AD,PF⊥BC
∴四边形ABFE,四边形DCFE是矩形
∴AE=BF,CF=DE
∴PA2﹣PD2=BP2﹣PC2.
拓展应用:∵PA2﹣PD2=BP2﹣PC2.
∴PA2﹣PB2=![]() c2.
c2.
∴PD2﹣PC2=![]() c2.
c2.
且PD2+PC2=c2.
∴PD=![]() c,PC=
c,PC=![]() c
c
∴![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数y1=x+2与反比例函数y2=![]() (x>0)的图象交于点A(a,5)
(x>0)的图象交于点A(a,5)
(1)确定反比例函数的表达式;
(2)结合图象,直接写出x为何值时,y1<y2
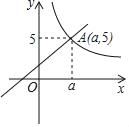
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两个共一个顶点的等腰Rt△ABC,Rt△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
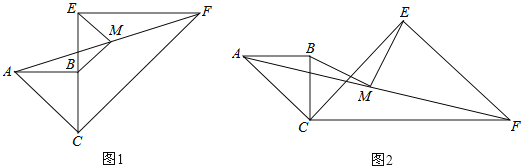
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
查看答案和解析>>
科目:初中数学 来源: 题型:
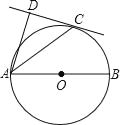
【题目】如图,AB为⊙O的直径,AB的长是4,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若cos∠DAC=![]() ,求弧BC的长.
,求弧BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第23个世界读书日前夕,我市某中学为了解本校学生的每周课外阅读时间![]() 用t表示,单位:小时
用t表示,单位:小时![]() ,采用随机抽样的方法进行问卷调查,调查结果按
,采用随机抽样的方法进行问卷调查,调查结果按![]() ,
,![]() ,
,![]() ,
,![]() 分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
分为四个等级,并依次用A,B,C,D表示,根据调查结果统计的数据,绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:
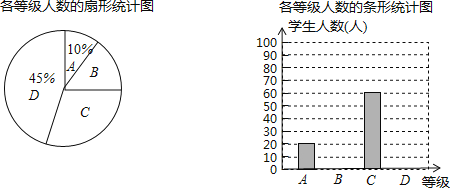
![]() 求本次调查的学生人数;
求本次调查的学生人数;
![]() 求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
求扇形统计图中等级B所在扇形的圆心角度数,并把条形统计图补充完整;
![]() 若该校共有学生1200人,试估计每周课外阅读时间满足
若该校共有学生1200人,试估计每周课外阅读时间满足![]() 的人数.
的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请大家阅读下面两段材料,并解答问题:
材料1:我们知道在数轴上表示4和1的两点之间的距离为3(如图1),而|4﹣1|=3,所以在数轴上表示4和1的两点之间的距离为|4﹣1|.
材料2:再如在数轴上表示4和﹣2的两点之间的距离为6(如图2)而|4﹣(﹣2)|=6,所以数轴上表示数4和﹣2的两点之间的距离|4﹣(﹣2)|.
(1)(如图3)根据上述规律,我们可以得出结论:在数轴上表示数a和数b两点之间的距离等于 .
(2)试一试,求在数轴上表示的数5![]() 与﹣4
与﹣4![]() 的两点之间的距离为 .
的两点之间的距离为 .
(3)已知数轴上表示数a的点M与表示数﹣1的点之间的距离为3,表示数b的点N与表示数2的点之间的距离为4,求M,N两点之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条东西走向的商业街上,依次有书店(记为A)、冷饮店(记为B)、鞋店(记为C),冷饮店位于鞋店西边50m处,鞋店位于书店东边60m处,王平先去书店,然后沿着这条街向东走了30m至D处,接着向西走50m到达E处.
(1)以A为原点、向东为正方向画数轴,在数轴上表示出上述A,B,C,D,E的位置;
(2)若在这条街上建一家超市,使超市与鞋店C分居E点两侧,且到E点的距离相等,问超市在冷饮店的什么方向?距离多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝元旦,学校准备举办一场“经典诵读”活动,某班准备网购一些经典诵读本和示读光盘,诵读本一套定价100元,示读光盘一张定价20元.元旦期间某网店开展促销活动,活动期间向客户提供两种优惠方案:
方案A:买一套诵读本送一张示读光盘;
方案B:诵读本和示读光盘都按定价的九折付款.
现某班级要在该网店购买诵读本10套和示读光盘x张(x>10),解答下列三个问题:
(1)若按方案A购买,共需付款 元(用含x的式子表示),
若按方案B购买,共需付款 元(用含x的式子表示);
(2)若需购买示读光盘15张(即x=15)时,请通过计算说明按哪种方案购买较为合算;
(3)若需购买示读光盘15张(即x=15)时,你还能给出一种更为省钱的购买方法吗?若能,请写出你的购买方法和所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com