
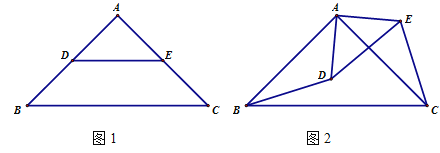
【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D,E在AB,AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
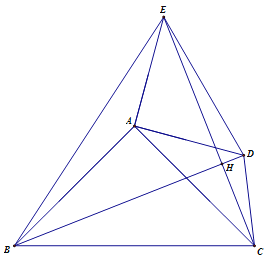
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点.
①若BD=![]() ,求四边形BCDE的面积;
,求四边形BCDE的面积;
②若AB=3,AD=2,设CD2=x,EB2=y,求y与x之间的函数关系式.
【答案】(1)BD=CE,BD⊥CE;
(2)BD⊥CE,理由见解析;
(3)①S四边形BCDE=![]() ;②y=26-x
;②y=26-x
【解析】试题分析:(1)由等腰直角三角形的性质即可得出;
(2)由边角边证得△ABD≌△ACE,由全等三角形的性质得出∠ABD=∠ACE,延长BD,由三角形内角和即可得∠CGF=∠BAF=90°,即可证得垂直;
(3)①易证△ABD≌△ACE,可得∠BHC=∠BAC=90°,即BD⊥CE,即可求得四边形BCDE的面积;
②由勾股定理等量代换即可求得y与x之间的函数关系式.
试题解析:(1)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC.AD=AE,
∴AB-AD=AC-AE,即:BD=CE,
∵BD、CE相交于点A,∠BAC=90°,
∴BD⊥CE;
(2)∵△ABC和△ADE都是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC-∠DAC, ∠CAE=∠DAE-∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,
延长BD,分别交AC,CE于F,G,BD=CE,
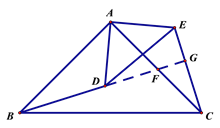
∵△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠AFB=∠GFC,
∴∠CGF=∠BAF=90°,即BD⊥CE;
(3)∵△ABC和△ADE都是等腰直角三角形,
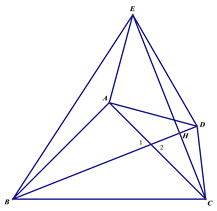
∴AB=AC,AD=AE,∠BAC=∠DAE=90°,
∵∠BAD=∠BAC+∠DAC,∠CAE=∠DAE+∠DAC,
∴∠BAD=∠CAE,
∴△ABD≌△ACE,
∴BD=CE,∠ABD=∠ACE
∵∠1=∠2
∴∠BHC=∠BAC=90°
∴S四边形BCDE=S△BCE+S△DCE= ![]() =
= ![]() =
=![]() ,
,
∵∠BHC=90°,
∴CD2+EB2=CH2+HD2+EH2+HB2=CH2+HB2+EH2+HD2=BC2+DE2=(![]() )2+(
)2+(![]() )2=26,
)2=26,
∴y=26-x.


科目:初中数学 来源: 题型:
【题目】已知△ABC≌△A′C′B′,∠B与∠C′,∠C与∠B′是对应角,有下列4个结论:①BC=C′B′;②AC=A′B′;③AB=A′B′;④∠ACB=∠A′B′C′,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高,越来越多的家庭采取分户式采暖,降低采暖用气价格的呼声强烈.某市物价局对市区居民管道天然气阶梯价格制度的规定作出了调整,调整后的付款金额y(单位:元)与年用气量(单位:m3)之间的函数关系如图所示:
(1)宸宸家年用气量是270m3,求付款金额.
(2)皓皓家去年的付款金额是1300元,求去年的用气量.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一组数据x1,x2,x3,x4,x5的平均数是2,方差是![]() ,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A. 2,![]() B. 2,1 C. 4,
B. 2,1 C. 4,![]() D. 4,3
D. 4,3
查看答案和解析>>
科目:初中数学 来源: 题型:
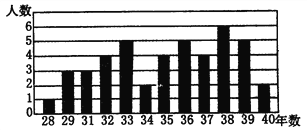
【题目】菲尔兹奖(The International Medals for Outstanding Discoveries in Mathematics)是国际数学联盟的国际数学家大会上颁发的奖项。每四年一次颁给有卓越贡献的年轻数学家,得奖者须在该年元旦前未满四十岁。菲尔兹奖被视为数学界的诺贝尔奖。本题中给出的条形图是截止到2002年44位费尔兹奖得主获奖时的年龄统计图。经计算菲尔兹奖得主获奖时的平均年龄是35岁。请根据条形图回答问题:
(1)费尔兹奖得主获奖时的年龄超过中位数的有多少人?
(2)费尔兹奖得主获奖时年龄的众数是多少?
(3)费尔兹奖得主获奖时的年龄高于平均年龄的人数占获奖人数的百分比是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com