
【题目】如图,∠AOB=90°,∠BOC=30°,射线OM平分∠AOC,ON平分∠BOC. 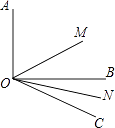
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,其他条件不变,求∠MON的度数;
(3)如果(1)中,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(4)从(1)、(2)、(3)的结果中,你能看出什么规律?
【答案】
(1)解:∠AOB=90°,∠BOC=30°,
∴∠AOC=90°+30=120°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=60°,∠CON=
∠AOC=60°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON=60°﹣15°=45°
(2)解:∠AOB=α,∠BOC=30°,
∴∠AOC=α+30°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() α+15°,∠CON=
α+15°,∠CON= ![]() ∠BOC=15°.
∠BOC=15°.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() α+15°﹣15°=
α+15°﹣15°= ![]() α
α
(3)解:∠AOB=90°,∠BOC=β,
∴∠AOC=β+90°.
由角平分线的性质可知:∠MOC= ![]() ∠AOC=
∠AOC= ![]() β+45°,∠CON=
β+45°,∠CON= ![]() ∠BOC=
∠BOC= ![]() β.
β.
∵∠MON=∠MOC﹣∠CON,
∴∠MON= ![]() β+45°﹣
β+45°﹣ ![]() β=45°
β=45°
(4)解:根据(1)、(2)、(3)可知∠MON= ![]() ∠BOC,与∠BOC的大小无关
∠BOC,与∠BOC的大小无关
【解析】(1)先求得∠AOC的度数,然后由角平分线的定义可知∠MOC=60°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(2)先求得∠AOC=α+30°,由角平分线的定义可知∠MOC= ![]() α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC=
α+15°,∠CON=15°,最后根据∠MON=∠MOC﹣∠CON求解即可;(3)先求得∠AOC=β+90°,由角平分线的定义可知∠MOC= ![]() β+15°,∠CON=
β+15°,∠CON= ![]() β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.
β,最后根据∠MON=∠MOC﹣∠CON求解即可;(4)根据计算结果找出其中的规律即可.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握角的运算(角之间可以进行加减运算;一个角可以用其他角的和或差来表示)的相关知识才是答题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个大型模板,设计要求BA与CD相交成30°角,DA与CB相交成20°角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检验模板是否合格?
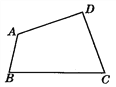
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数 y=(k-2)x 中,y 随 x 的增大而减小,则 k 的取值范围是( )
A. k≥2 B. k≤2 C. k>2 D. k<2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快4G网络建设,某市电信运营企业根据自身发展规划,2014年计划完成投资28000000元,将28000000用科学记数法可表示为( )
A. 2.8×104B. 0.28×108C. 2.8×107D. 28×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P关于x轴的对称点P1的坐标是(2,3),那么点P关于原点的对称点P2的坐标是( )
A.(﹣3,﹣2)
B.(2,﹣3)
C.(﹣2,﹣3)
D.(﹣2,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com