
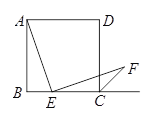
【题目】如图,已知边长为4的正方形ABCD,E是BC边上一动点(与B、C不重合),连结AE,作EF⊥AE交∠BCD的外角平分线于F,设BE=x,△ECF的面积为y,下列图象中,能表示y与x的函数关系的图象大致是( )
A. 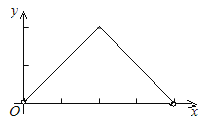 B.
B. 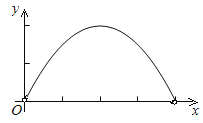
C. 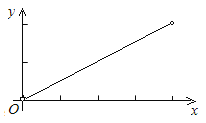 D.
D. 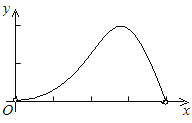
科目:初中数学 来源: 题型:
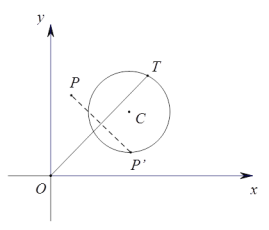
【题目】在平面直角坐标系![]() 中,对于点
中,对于点![]() 和
和![]() ,给出如下定义:若
,给出如下定义:若![]() 上存在一点
上存在一点![]() 不与
不与![]() 重合,使点
重合,使点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在
在![]() 上,则称
上,则称![]() 为
为![]() 的反射点.下图为
的反射点.下图为![]() 的反射点
的反射点![]() 的示意图.
的示意图.
(1)已知点![]() 的坐标为
的坐标为![]() ,
,![]() 的半径为
的半径为![]() ,
,
①在点![]() ,
,![]() ,
,![]() 中,
中,![]() 的反射点是____________;
的反射点是____________;
②点![]() 在直线
在直线![]() 上,若
上,若![]() 为
为![]() 的反射点,求点
的反射点,求点![]() 的横坐标的取值范围;
的横坐标的取值范围;
(2)![]() 的圆心在
的圆心在![]() 轴上,半径为
轴上,半径为![]() ,
,![]() 轴上存在点
轴上存在点![]() 是
是![]() 的反射点,直接写出圆心
的反射点,直接写出圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,赛后随机抽查了部分学生的成绩(得分取正整数,满分为100分)进行统计分析,并制作成图表:
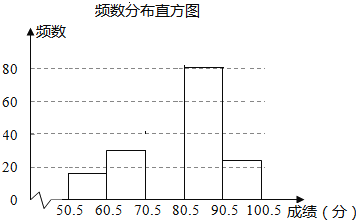
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | m | 0.25 |
四 | 80.5~90.5 | 80 | n |
五 | 90.5~100.5 | 24 | 0.12 |
请根据以上图表提供的信息,解答下列可题:
(1)这次随机抽查了______名学生,表中的数m=______,n=______;此样本中成绩的中位数落在第______组内;若绘制扇形统计图,则在修中“第三组”所对应扇形的圆心角的度数是______
(2)补全频数直方图;
(3)若成绩超过80分为优秀,请你估计该校八年级学生中汉字听写能力优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,顶点为
,顶点为![]() .
.
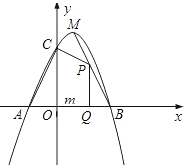
(1)求二次函数的解析式;
(2)点![]() 为线段
为线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,若
,若![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
(3)探索:线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,求出点
为等腰三角形?如果存在,求出点![]() 的坐标;如果不存在,请说呀理由.
的坐标;如果不存在,请说呀理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
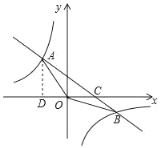
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (n≠0)的图象交于第二、四象限内的A、B两点与x轴交于点C,点B坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=
(n≠0)的图象交于第二、四象限内的A、B两点与x轴交于点C,点B坐标为(m,﹣1),AD⊥x轴,且AD=3,tan∠AOD=![]()
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求S△AOC﹣S△BOC的值;
(3)点E是x轴上一点,且△AOE是等腰三角形请直接写出满足条件的E点的个数(写出个数即可,不必求出E点坐标).
查看答案和解析>>
科目:初中数学 来源: 题型:
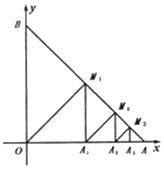
【题目】在平面直角坐标系中,点![]() 在
在![]() 轴正半轴上,点
轴正半轴上,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() 为坐标原点,
为坐标原点,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() :过点
:过点![]() 作
作![]() 于点
于点![]() :过点
:过点![]() 作
作![]() 于点
于点![]() :过点
:过点![]() 作
作![]() 于点
于点![]() …以此类推,点
…以此类推,点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
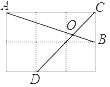
A. ![]() B. 2C. 1D.
B. 2C. 1D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
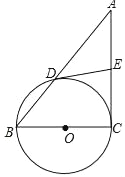
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,过点D作⊙O的切线DE交AC于点E.
(1)求证:∠A=∠ADE;
(2)若AB=25,DE=10,弧DC的长为a,求DE、EC和弧DC围成的部分的面积S.(用含字母a的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com