
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么称这个正整数为“巧数”,如:![]() ,
,![]() ,
,![]() ,因此4,12,20这三个数都是“巧数”.
,因此4,12,20这三个数都是“巧数”.
(1)400和2020这两个数是“巧数”吗?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 取正整数),由这两个连续偶数构造的“巧数”是4的倍数吗?为什么?
取正整数),由这两个连续偶数构造的“巧数”是4的倍数吗?为什么?
(3)求介于50到101之间所有“巧数”之和.
【答案】(1)400不是“巧数”,2020是“巧数”,理由见解析;(2)是,理由见解析;(3)532.
【解析】
(1)根据“巧数”的定义进行判断即可;
(2)列出这两数的平方差,运用平方差公式进行计算,对结果进行分析即可;
(3)介于50到100之间的所有“巧数”中,最小的为:142-122=52,最大的为:262-242=100,将它们全部列出不难求出他们的和.
解:(1)400不是“巧数”,2020是“巧数”.原因如下:
因为![]() ,故400不是“巧数”,
,故400不是“巧数”,
因为2020=5062-5042,故2020是“巧数”;
(2)![]()
∵n为正整数,
∴2n-1一定为正整数,
∴4(2n-1)一定能被4整除,
即由这两个连续偶数构造的“巧数”是4的倍数;
(3)介于50到100之间的所有“巧数”之和,
S=(142-122)+(162-142)+(182-162)+…+(262-242)=262-122=532.
故答案是:532.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b'),给出如下定义:
若b'=![]() ,则称点Q为点P的限变点.例如:点(3,﹣2)的限变点的坐标是(3,﹣2),点(﹣1,5)的限变点的坐标是(﹣1,﹣5).
,则称点Q为点P的限变点.例如:点(3,﹣2)的限变点的坐标是(3,﹣2),点(﹣1,5)的限变点的坐标是(﹣1,﹣5).
(1)①点(﹣![]() ,1)的限变点的坐标是 ;
,1)的限变点的坐标是 ;
②在点A(﹣1,2),B(﹣2,﹣1)中有一个点是函数y=![]() 图象上某一个点的限交点,这个点是 ;
图象上某一个点的限交点,这个点是 ;
(2)若点P在函数y=﹣x+3的图象上,当﹣2≤x≤6时,求其限变点Q的纵坐标b'的取值范围;
(3)若点P在关于x的二次函数y=x2﹣2tx+t2+t的图象上,其限变点Q的纵坐标b'的取值范围是b'≥m或b'<n,其中m>n.令s=m﹣n,求s关于t的函数解析式及s的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家在“吾悦广场”购买了一间商铺,准备承包给甲、乙两家装修公司进行店面装修,经调查:甲公司单独完成该工程的时间是乙公司的2倍,已知甲、乙两家公司共同完成该工程建设需20天;若甲公司每天所需工作费用为650元,乙公司每天所需工作费用为1200元,若从节约资金的角度考虑,则应选择哪家公司更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
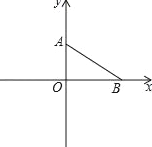
【题目】如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣3|+![]() =0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
=0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.
(1)求OA、OB的长;
(2)连接PB,设△POB的面积为S,用t的式子表示S;
(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
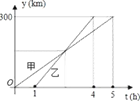
【题目】甲、乙两车从A城出发沿一条笔直公路匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离![]() (千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.
(1)A,B两城相距 千米,乙车比甲车早到 小时;
(2)甲车出发多长时间与乙车相遇?
(3)若两车相距不超过20千米时可以通过无线电相互通话,则两车都在行驶过程中可以通过无线电通话的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,点
,点![]() 分别是
分别是![]() 轴,
轴,![]() 轴上两个动点,直角边
轴上两个动点,直角边![]() 交
交![]() 轴于点
轴于点![]() ,斜边
,斜边![]() 交
交![]() 轴于点
轴于点![]() .
.
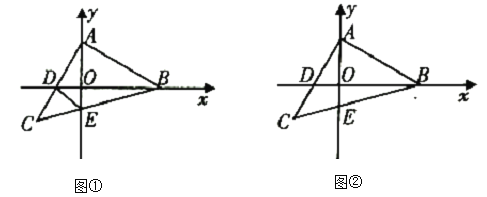
(1)如图①,当等腰![]() 运动到使点
运动到使点![]() 恰为
恰为![]() 中点时,连接
中点时,连接![]() ,求证:
,求证:![]() ;
;
(2)如图②,当等腰![]() 运动到使
运动到使![]() 时,
时,![]() 点的横坐标为
点的横坐标为![]() ,
,![]() .在
.在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,已知点![]() 、点
、点![]() ,动点
,动点![]() 从点
从点![]() 开始在线段
开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,同时动点
移动,同时动点![]() 从点
从点![]() 开始在线段
开始在线段![]() 上以每秒
上以每秒![]() 个单位长度的速度向点
个单位长度的速度向点![]() 移动,设点
移动,设点![]() 、
、![]() 移动的时间为
移动的时间为![]() 秒.
秒.
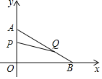
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 当
当![]() 为何值时,
为何值时,![]() 的面积为
的面积为![]() 个平方单位?
个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个箱子,其中甲箱内有![]() 颗球,分别标记号码
颗球,分别标记号码![]() ,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出
,且号码为不重复的整数,乙箱内没有球.已知小育从甲箱内拿出![]() 颗球放入乙箱后,乙箱内球的号码的中位数为
颗球放入乙箱后,乙箱内球的号码的中位数为![]() .若此时甲箱内有
.若此时甲箱内有![]() 颗球的号码小于
颗球的号码小于![]() ,有
,有![]() 颗球的号码大于
颗球的号码大于![]() ,若他们的中位数都为
,若他们的中位数都为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在
在![]() 的
的![]() 边上,
边上,![]() 交
交![]() 于
于![]() ,
,![]() 交
交![]() 于
于![]() ,若添加条件________,则四边形
,若添加条件________,则四边形![]() 是矩形;若添加条件________,则四边形
是矩形;若添加条件________,则四边形![]() 是菱形;若添加条件________,则四边形
是菱形;若添加条件________,则四边形![]() 是正方形.
是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com