
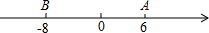 已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度变为M点的3倍.
已知数轴上两点A、B对应的数分别是6,-8,M、N为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度变为M点的3倍.分析 (1)设经过x秒点M与点N相距54个单位,由点M从A点出发速度为每秒2个单位,点N从点B出发速度为M点的3倍,得出2x+6x+14=54求出即可;
(2)首先设经过t秒点M与点N相距4个单位,得出(2t+6)-(6t-8)=4或(6t-82)-(2t+6)=4,进而求出即可.
解答 解:(1)设经过x秒点M与点N相距54个单位.
依题意可列方程为:2x+6x+14=54,
解方程,得x=5.
答:经过5秒点M与点N相距54个单位.(算术方法对应给分)
(2)设经过t秒点M与点N相距4个单位.
(2t+6)-(6t-8)=4或(6t-8)-(2t+6)=4,
解得t=2.5或t=4.5.
答:经过2.5或4.5秒时间点M与点N相距4个单位.
点评 此题主要考查了数轴、一元一次方程的应用,根据已知点运动速度得出以及距离之间的关系得出等式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.
某中学八(1)班共50名同学开展了“我为灾区献爱心”捐款活动.小明将捐款情况进行了统计,并绘制成如图的条形统计图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com