
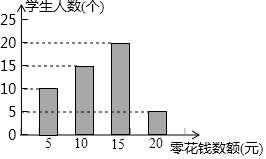
 某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.
某教师为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行统计调查,并绘制了统计表及统计图,如图所示.分析 (1)根据加权平均数的计算公式计算可得;
(2)用样本中零花钱数额为20元的人数所占的比例乘以360°即可得;
(3)用平均数乘以总人数,再乘以75%即可得.
解答 解:(1)平均数是$\frac{1}{50}$×(5×10+10×15+15×20+20×5)=12元,
故答案为:12;
(2)一周内的零花钱数额为20元的人数所占的圆心角度数是360°×$\frac{5}{50}$=36°,
故答案为:36°;
(3)1500×12×75%=13500元,
答:估计该校学生每周在学校超市消费的零花钱总金额为13500元.
点评 此题考查了条形统计图、扇形统计图以及用样本估计总体,弄清题中的数据是解本题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
| A. | 负数 | B. | 非正数 | C. | 正数 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
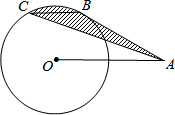 如图,A是半径为2的⊙O外的一点,OA=4,AB切⊙O于点B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{2}{3}$π.
如图,A是半径为2的⊙O外的一点,OA=4,AB切⊙O于点B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{2}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
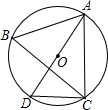 如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,
如图,⊙O是△ABC的外接圆,AD是⊙O的直径,连接CD,若⊙O的半径r=5,AC=5$\sqrt{3}$,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com