
| A. | ①② | B. | ①③④ | C. | ③④ | D. | ①②④ |
分析 ①正确.根据图中的信息,求出BE、AD的值即可判断.
②正确.根据SAS即可判断.
③错误.求出BE+DE+CD的值,可知点P运动了22秒.
④错误.当t=$\frac{27}{2}$秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,由此即可判断.
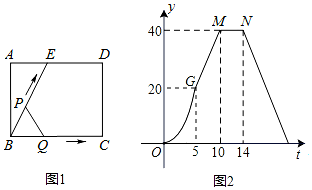
解答 解:察图象可知,AD=BC=5×2=10,BE=1×10=10,ED=4×1=4,AE=10-4=6,
∴BE=BC,故①正确,
如图1中,当t=6秒时,点P在BE上,点Q静止于点C处,
在△ABE与△PQB中,
$\left\{\begin{array}{l}{AE=PB=6}\\{∠1=∠2}\\{BE=BC}\end{array}\right.$,
∴△ABE≌△PQB(SAS),故②正确,
在Rt△ABE中,AB=$\sqrt{B{E}^{2}-A{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∴BE+DE+DC=10+4+8=22,
∴点P运动了22秒,故③错误,
当t=$\frac{27}{2}$秒时,点P在线段DE上,点Q与点C重合,此时∠PQB≠90°,
∴△ABE与△QBP不相似,故④错误.
∴①②正确,
故选A.
点评 本题考查二次函数综合题、矩形的性质、全等三角形的判定和性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是读懂图中信息,利用信息解决问题,属于中考压轴题.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:选择题
| A. | (x-$\frac{3}{2}$)2=16 | B. | 2(x-$\frac{3}{4}$)2=$\frac{1}{16}$ | C. | (x-$\frac{3}{4}$)2=$\frac{1}{16}$ | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x(x+1)=28 | B. | x(x-1)=28 | C. | $\frac{1}{2}$x(x+1)=28 | D. | $\frac{1}{2}$x(x-1)=28 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
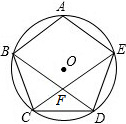 如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.
如图,五边形ABCDE内接于⊙O,且$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$=$\widehat{DE}$=$\widehat{AE}$,BD和CE相交于点F,不添加辅助线,则图中有5个等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-2>y-2 | B. | x+1>y+1 | C. | $\frac{x}{5}$>$\frac{y}{5}$ | D. | -5x>-5y |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com