


科目:初中数学 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
| 1 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
| p |
| q |
| 3 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 8 |
查看答案和解析>>
科目:初中数学 来源:2012-2013学年重庆万州二中八年级上学期期中考试数学试卷(带解析) 题型:单选题
任何一个正整数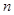 都可以进行这样的分解:
都可以进行这样的分解: (
( 是正整数,且
是正整数,且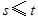 ),如果
),如果 在
在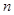 的所有这种分解中两因数之差的绝对值最小,我们就称
的所有这种分解中两因数之差的绝对值最小,我们就称 是
是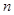 的最佳分解,并规定:
的最佳分解,并规定: .例如18可以分解成
.例如18可以分解成 ,
, ,
, 这三种,这时就有
这三种,这时就有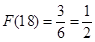 .给出下列关于
.给出下列关于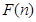 的说法:(1)
的说法:(1) ;(2)
;(2)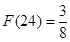 ;(3)
;(3)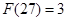 ;(4)若
;(4)若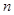 是一个完全平方数,则
是一个完全平方数,则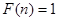 .其中正确说法的个数是( )
.其中正确说法的个数是( )
A.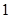 | B.4 | C.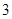 | D.2 |
查看答案和解析>>
科目:初中数学 来源:2007年初中毕业升学考试(江苏无锡卷)数学(解析版) 题型:选择题
任何一个正整数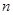 都可以进行这样的分解:
都可以进行这样的分解: 如果
如果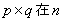 的所有这种分解中两因数之差的绝对值最小,我们就称
的所有这种分解中两因数之差的绝对值最小,我们就称 的最佳分解,并规定:
的最佳分解,并规定: 这三种,这时就有
这三种,这时就有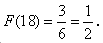 给出下列
给出下列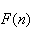 的说法:
的说法: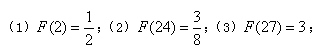 (4)若n是一个完全平方数,则
(4)若n是一个完全平方数,则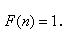 .其中正确说法的个数是( )
.其中正确说法的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com