
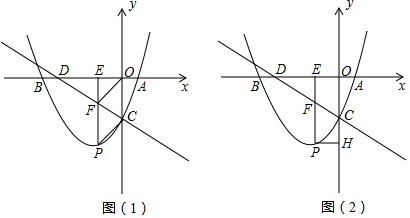
分析 (1)将点A和点C的坐标代入抛物线的解析式可得到关于a、c的方程组,然后解方程组求得a、c的值即可;
(2)设P(m,$\frac{1}{5}$m2+$\frac{8}{5}$m-4),则F(m,-$\frac{1}{2}$m-4),则PF=-$\frac{1}{5}$m2-$\frac{21}{10}$m,当PF=OC时,四边形PCOF是平行四边形,然后依据PF=OC列方程求解即可;
(3)①先求得点D的坐标,然后再求得AC、DC、AD的长,最后依据勾股定理的逆定理求解即可;②分为△ACD∽△CHP、△ACD∽△PHC两种情况,然后依据相似三角形对应成比例列方程求解即可
解答 解:(1)由题意得:$\left\{\begin{array}{l}{4a+\frac{8}{5}×2+c=0}\\{c=-4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{1}{5}}\\{c=-4}\end{array}\right.$,
∴抛物线的表达式为y=$\frac{1}{5}$x2+$\frac{8}{5}$x-4.
(2)设P(m,$\frac{1}{5}$m2+$\frac{8}{5}$m-4),则F(m,-$\frac{1}{2}$m-4).
∴PF=(-$\frac{1}{2}$m-4)-($\frac{1}{5}$m2+$\frac{8}{5}$m-4)=-$\frac{1}{5}$m2-$\frac{21}{10}$m.
∵PE⊥x轴,
∴PF∥OC.
∴PF=OC时,四边形PCOF是平行四边形.
∴-$\frac{1}{5}$m2-$\frac{21}{10}$m=4,解得:m=-$\frac{5}{2}$或m=-8.
当m=-$\frac{5}{2}$时,$\frac{1}{5}$m2+$\frac{8}{5}$m-4=-$\frac{27}{4}$,
当m=-8时,$\frac{1}{5}$m2+$\frac{8}{5}$m-4=-4.
∴点P的坐标为(-$\frac{5}{2}$,-$\frac{27}{4}$)或(-8,-4).
(3)①证明:把y=0代入y=-$\frac{1}{2}$x-4得:-$\frac{1}{2}$x-4=0,解得:x=-8.
∴D(-8,0).
∴OD=8.
∵A(2,0),C(0,-4),
∴AD=2-(-8)=10.
由两点间的距离公式可知:AC2=22+42=20,DC2=82+42=80,AD2=100,
∴AC2+CD2=AD2.
∴△ACD是直角三角形,且∠ACD=90°.
②由①得∠ACD=90°.
当△ACD∽△CHP时,$\frac{AC}{CD}$=$\frac{CH}{HP}$,即$\frac{2\sqrt{5}}{4\sqrt{5}}$=$\frac{-\frac{1}{5}{n}^{2}-\frac{8}{5}n}{-n}$或$\frac{2\sqrt{5}}{4\sqrt{5}}$=$\frac{\frac{1}{5}{n}^{2}+\frac{8}{5}n}{-n}$,
解得:n=0(舍去)或n=-5.5或n=-10.5.
当△ACD∽△PHC时,$\frac{AC}{CD}$=$\frac{PH}{CH}$,即$\frac{2\sqrt{5}}{4\sqrt{5}}$=$\frac{-n}{-\frac{1}{5}{n}^{2}-\frac{8}{5}n}$或即$\frac{2\sqrt{5}}{4\sqrt{5}}$=$\frac{-n}{\frac{1}{5}{n}^{2}+\frac{8}{5}n}$.
解得:n=0(舍去)或n=2或n=-18.
综上所述,点P的横坐标为-5.5或-10.5或2或-18时,使得以点P、C、H为顶点的三角形与△ACD相似.
点评 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、平行四边形的性质、勾股定理的逆定理、相似三角形的性质,依据平行线的对边相等列出关于m的方程是解答问题(2)的关键,利用相似三角形的性质列出关于n的方程是解答问题(3)的关键.


科目:初中数学 来源: 题型:解答题
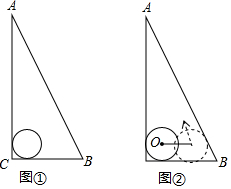 如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
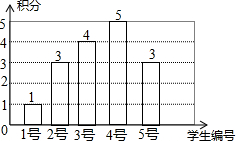 编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.
编号为1~5号的5名学生进行定点投篮,规定每人投5次,每命中1次记1分,没有命中记0分,如图是根据他们各自的累积得分绘制的条形统计图.之后来了第6号学生也按同样记分规定投了5次,其命中率为40%.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
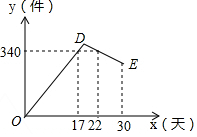 某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.
某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
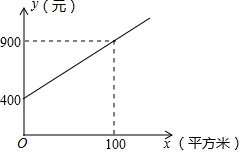 甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com