
 (n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.
(n为自然数),问:是否存在自然数n,使代数式19x2+36xy+19y2的值为1 998?若存在,求出n;若不存在,请说明理由.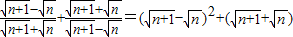 2
2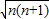 +n+n+1+n+2
+n+n+1+n+2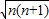 =4n+2.
=4n+2.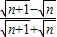 •
•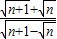 =1.
=1.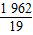 .
.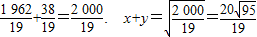 .
.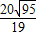 不为整数.
不为整数.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com