
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���B��a��b���ǵ�һ������һ�㣬��a��b�����ʽa2-6a+9+|b-1|=0��

��1�����B�����ꣻ
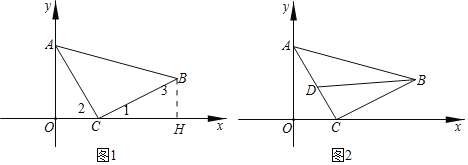
��2����ͼ������C��ÿ��1����λ���ȵ��ٶȴ�O���������x��������᷽���˶���ͬʱ����A��ÿ��2����λ���ȵ��ٶȴ�O���������y��������᷽���˶������˶���ʱ��Ϊt�룬��tΪ��ֵʱ����ABC��ABΪб�ߵĵ���ֱ�������Σ�
��3����ͼ���ڣ�2���������£�����ABC��ƽ����BD����BD�ij�Ϊm����ADB�����ΪS�����ú�m��ʽ�ӱ�ʾS��
���𰸡���1��B��3��1������2����t=1ʱ����ABC����ABΪб�ߵĵ���ֱ�������Σ���3��![]()
��������
��1�����ݷǸ��Եó�a��b��ֵ��������ɣ�
��2����B��BH��x����H�����ݵ���ֱ�������ε����ʺ�ȫ�������ε��ж������ʽ�ɣ�
��3������A��AF��DB����BD�ӳ�����F��AF�ӳ��߽�BC���ӳ����ڵ�E������ȫ�������ε��ж������ʽ�ɣ�
�⣺��1����a2-6a+9+|b-1|=0��
�ࣨa-3��2+|b-1|=0
�ң�a-3��2��0��|b-1|��0
��a-3=0��b-1=0
��a=3��b=1
��B��3��1����
��2����B��BH��x����H
��B��3��1����
��BH=1
�������OA=2t��OC=t
�ߡ�ACB����ABб�ߵĵ���ֱ��������
��AC=BC��
��ACB=90��
���1+��2=90��
��BH��x�ᣬ
���OHB=90��
���1+��3=90��
���2=��3
���AOC=��CHB=90��
����AOC����CHB��
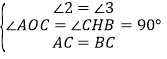 ��
��
���AOC�ա�CHB��AAS��
��OC=BH
��t=1��
�൱t=1ʱ����ABC����ABΪб�ߵĵ���ֱ�������Σ�
��3������A��AF��DB����BD�ӳ�����F��AF�ӳ��߽�BC���ӳ����ڵ�E��

�ߡ�AFB=��ACB=90��
���1+��E=90��
��2+��E=90��
���2=��1
����DCB����ECA��
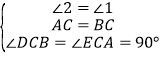 ��
��
���DCB�ա�ECA��ASA��
��AE=DB=m
����BFA����BFE��
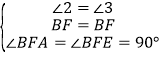 ��
��
���BFA�ա�BFE��ASA��
��AF=EF=![]()
��![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
��1��23��17������7��+����16����
��2��-5+6�£�-2����![]() ��
��
��3��-36��![]() ��
��
��4����23+|5��8|+24�£���3����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() ��һԪ���η���m
��һԪ���η���m ![]() +2x��1=0����������ȵ�ʵ��������
+2x��1=0����������ȵ�ʵ�������� ![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A.m����1
B.m��1
C.m��1��m��0
D.m����1��m��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η��̣�x-2����x-3��=m��ʵ����x1 �� x2 �� ��x1![]() x2�����н��ۣ�
x2�����н��ۣ�
��x1=2��x2=3����m> ![]() ���۶��κ���y=��x-x1����x-x2��+m��ͼ����x�ύ�������Ϊ��2��0���ͣ�3��0����
���۶��κ���y=��x-x1����x-x2��+m��ͼ����x�ύ�������Ϊ��2��0���ͣ�3��0����
������ȷ�Ľ�����������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
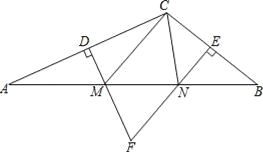
����Ŀ����ͼ������ABC�У�DM��EN�ֱ�ֱƽ��AC��BC����AB��M��N���㣬DM��EN�ཻ�ڵ�F��
��1������CMN���ܳ�Ϊ15cm����AB�ij���
��2������MFN=70��������MCN�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3��BC=5����BΪԲ��BCΪ�뾶������AD�ڵ�E������CE����BF��CE������ΪF����tan��FBC��ֵΪ�� ��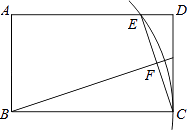
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
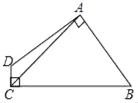
����Ŀ����ͼ���ı���ABCD�У�AB��AD��AC��5����DAB����DCB��90�㣬���ı���ABCD�����Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���![]() �У�
��![]() ��
��![]() .
.
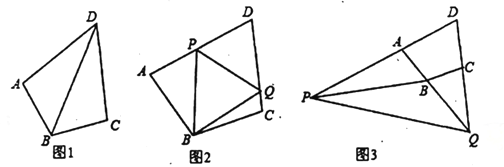
(1)��ͼ1������![]() ����
����![]() ����֤��
����֤��![]() .
.
(2)��ͼ2����![]() �ֱ����߶�
�ֱ����߶�![]() �ϣ�����
�ϣ�����![]() ����֤��
����֤��![]() ;
;
(3)����![]() ��
��![]() ���ӳ����ϣ���
���ӳ����ϣ���![]() ��
��![]() ���ӳ����ϣ���ͼ3��ʾ����Ȼ����
���ӳ����ϣ���ͼ3��ʾ����Ȼ����![]() ����д��
�����![]() ��
��![]() ��������ϵ��������֤�����̣�
��������ϵ��������֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��¥�Ķ�������һ������CD��С����ɽ�µ��½�A����ù���Ƶײ�D������Ϊ60�㣮������AB�����ߵ�B����ù���ƶ���C������Ϊ45�㣬��֪ɽ��AB���¶� ![]() ��AB=10�ף�AE=15�ף�
��AB=10�ף�AE=15�ף�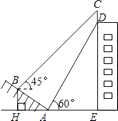
��1�����B��ˮƽ��AE�ĸ߶�BH��
��2��������CD�ĸ߶ȣ�
��������ĸ߶Ⱥ��Բ��ƣ������ȷ��0��1�ף��ο����ݣ� ![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com