

分析 (1)由四边形OEFG是正方形,得到ME=$\frac{1}{2}$GE,根据三角形的中位线的性质得到CD∥GE,CD=$\frac{1}{2}$GE,求得CD=GE,即可得到结论;
(2)如图2,延长E′D交AG′于H,由四边形ABCD是正方形,得到AO=OD,∠AOD=∠COD=90°,由四边形OEFG是正方形,得到OG′=OE′,∠E′OG′=90°,由旋转的性质得到∠G′OD=∠E′OC,求得∠AOG′=∠COE′,根据全等三角形的性质得到AG′=DE′,∠AG′O=∠DE′O,即可得到结论;
(3)分类讨论,根据三角形的外角的性质和等腰三角形的性质即可得到结论.
解答 证明:(1)∵四边形OEFG是正方形,
∴ME=$\frac{1}{2}$GE,
∵OG=2OD、OE=2OC,
∴CD∥GE,CD=$\frac{1}{2}$GE,
∴CD=GE,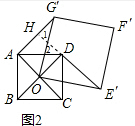
∴四边形CDME是平行四边形;
(2)如图2,延长E′D交AG′于H,
∵四边形ABCD是正方形,
∴AO=OD,∠AOD=∠COD=90°,
∵四边形OEFG是正方形,
∴OG′=OE′,∠E′OG′=90°,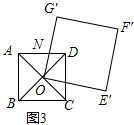
∵将正方形OEFG绕点O逆时针旋转,得到正方形OE′F′G′,
∴∠G′OD=∠E′OC,
∴∠AOG′=∠COE′,
在△AG′O与△ODE′中,$\left\{\begin{array}{l}{OA=OD}\\{∠AOG′=∠DOE′}\\{OG′=OE′}\end{array}\right.$,
∴△AG′O≌△ODE′
∴AG′=DE′,∠AG′O=∠DE′O,
∵∠1=∠2,
∴∠G′HD=∠G′OE′=90°,
∴AG′⊥DE′;
(3)①正方形OE′F′G′的边OG′与正方形ABCD的边AD相交于点N,如图3,
Ⅰ、当AN=AO时,
∵∠OAN=45°,
∴∠ANO=∠AON=67.5°,
∵∠ADO=45°,
∴α=∠ANO-∠ADO=22.5°;
Ⅱ、当AN=ON时,
∴∠NAO=∠AON=45°,
∴∠ANO=90°,
∴α=90°-45°=45°;
②正方形OE′F′G′的边OG′与正方形ABCD的边AB相交于点N,如图4,
Ⅰ、当AN=AO时,
∵∠OAN=45°,
∴∠ANO=∠AON=67.5°,
∵∠ADO=45°,
∴α=∠ANO+90°=112.5°;
Ⅱ、当AN=ON时,
∴∠NAO=∠AON=45°,
∴∠ANO=90°,
∴α=90°+45°=135°,
Ⅲ、当AN=AO时,旋转角a=∠ANO+90°=67.5+90=157.5°,
综上所述:若△AON是等腰三角形时,α的值是22.5°或45°或112.5°或135°或157.5°.
点评 本题主要考查了正方形的性质、全等三角形的判定与性质、锐角三角函数、旋转变换的性质的综合运用,有一定的综合性,分类讨论当△AON是等腰三角形时,求α的度数是本题的难点.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
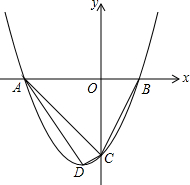 已知:二次函数y=ax2+bx+c的图象与x轴相交于A(-4,0),B(2,0)两点,与y轴相交于点C(0,-4),点D为抛物线的顶点.
已知:二次函数y=ax2+bx+c的图象与x轴相交于A(-4,0),B(2,0)两点,与y轴相交于点C(0,-4),点D为抛物线的顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 年龄(单位:岁) | 12 | 13 | 14 | 15 |
| 人数 | 12 | 14 | 18 | 6 |
| A. | 13岁、14岁 | B. | 14岁,14岁 | C. | 14岁,13岁 | D. | 14岁,15岁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 合格为了让学生更好地树立“安全第一,预防为主”的思想,河图中心学校开展了“2015秋季校园安全知识竞赛”活动,若该知识竞赛的成绩分为A(优秀),B(良好),C(合格),D(不合格)四个等级,王老师从中抽取若干名学生的成绩进行统计,并将统计结果绘制成如图所示的扇形统计图,若成绩为良好的学生比不合格的多5名,则成绩优秀的学生比合格的( )
合格为了让学生更好地树立“安全第一,预防为主”的思想,河图中心学校开展了“2015秋季校园安全知识竞赛”活动,若该知识竞赛的成绩分为A(优秀),B(良好),C(合格),D(不合格)四个等级,王老师从中抽取若干名学生的成绩进行统计,并将统计结果绘制成如图所示的扇形统计图,若成绩为良好的学生比不合格的多5名,则成绩优秀的学生比合格的( )| A. | 多5名 | B. | 少5名 | C. | 多10名 | D. | 少10名 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 2015年我国世界环境日的主题是“践行绿色生活”.为更好地倡导市民关注环境、节约用水,政府对某小区500户家庭的用水情况进行了调查,调查小组随机抽查了其中100户家庭的月平均用水量(单位:吨),并将调查结果制成了如图所示的统计图.
2015年我国世界环境日的主题是“践行绿色生活”.为更好地倡导市民关注环境、节约用水,政府对某小区500户家庭的用水情况进行了调查,调查小组随机抽查了其中100户家庭的月平均用水量(单位:吨),并将调查结果制成了如图所示的统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com