
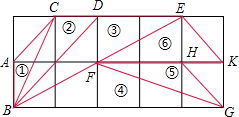
 如图,在正方形网格上有6个斜三角形:
如图,在正方形网格上有6个斜三角形:分析 两个三角形三条边对应成比例,两个三角形相似,据此即可解答.
解答 解:设第个小正方形的边长为1,则△ABC的各边长分别为1、$\sqrt{2}$、$\sqrt{5}$.则
②△BCD的各边长分别为1、$\sqrt{5}$、2 $\sqrt{2}$;
③△BDE的各边长分别为2、2 $\sqrt{5}$、2 $\sqrt{2}$(为△ABC对应各边长的2倍);
④△BFG的各边长分别为5、$\sqrt{5}$、$\sqrt{10}$(为△ABC对应各边长的 $\sqrt{5}$倍);
⑤△FGH的各边长分别为2、$\sqrt{2}$、$\sqrt{10}$(为△ABC对应各边长的 $\sqrt{2}$倍);
⑥△EFK的各边长分别为3、$\sqrt{2}$、$\sqrt{5}$.
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤.
故答案为:③④⑤.
点评 此题主要考查了相似三角形的判定方法;熟记三组对应边的比相等的两个三角形相似是解决问题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
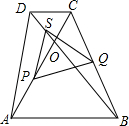 如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.
如图,在等腰梯形ABCD中,AB∥DC,AD=BC,对角线AC与BD相交于点O,∠ACD=60°,点S、P、Q分别为OD、OA、BC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
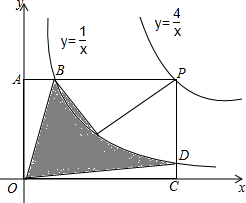 如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )
如图,点P为反比例函数y=$\frac{4}{x}$(x>0)图象上一点,过点P作y轴的垂线,交双曲线y=$\frac{1}{x}$于点B,交y轴于点A,过点P作x轴的垂线,交双曲线y=$\frac{1}{x}$于点D,交x轴于点C,连接OP交双曲线y=$\frac{1}{x}$于点E,则连接BO,OD,DE,EB而围成的阴影部分面积为( )| A. | 1 | B. | $\frac{5}{4}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )
在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1;…,按这样的规律进行下去,第2016个正方形的面积为( )| A. | 5×($\frac{3}{2}$)2016 | B. | 5×($\frac{9}{4}$)2016 | C. | 5×($\frac{9}{4}$)2015 | D. | 5×($\frac{3}{2}$)4032 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.
已知:如图,AB=AC,点D是BC的中点,AD=AE,AE⊥BE,垂足为E,连结DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
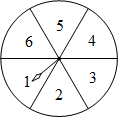 如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.
如图,转盘被等分成6个扇形,每个扇形上依次标有数字1,2,3,4,5,6.在游戏中特别规定:当指针指向边界时,重新转动转盘.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com