
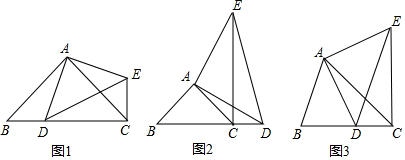
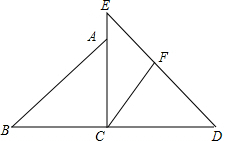
分析 (1)①根据∠BAD=∠CAE,BA=CA,AD=AE,运用“SAS”证明△ABD≌△ACE,根据全等三角形性质得出对应边相等,对应角相等,即可得到线段CE、BD之间的关系;
②先根据“SAS”证明△ABD≌△ACE,再根据全等三角形性质得出对应边相等,对应角相等,即可得到①中的结论仍然成立;
(2)先过点A作AG⊥AC交BC于点G,画出符合要求的图形,再结合图形判定△GAD≌△CAE,得出对应角相等,即可得出结论.
解答 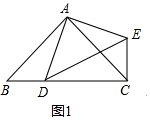 解:(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
解:(1)CE与BD位置关系是CE⊥BD,数量关系是CE=BD.
理由:如图1,∵∠BAD=90°-∠DAC,∠CAE=90°-∠DAC,
∴∠BAD=∠CAE.
又 BA=CA,AD=AE,
∴△ABD≌△ACE (SAS)
∴∠ACE=∠B=45°且 CE=BD.
∵∠ACB=∠B=45°,
∴∠ECB=45°+45°=90°,即 CE⊥BD.
故答案为:垂直,相等;
②都成立.
∵∠BAC=∠DAE=90°,
∴∠BAC+∠DAC=∠DAE+∠DAC,
∴∠BAD=∠CAE,
在△DAB与△EAC中,
$\left\{\begin{array}{l}{AD=AE}\\{∠BAD=∠CAE}\\{AB=AC}\end{array}\right.$
∴△DAB≌△EAC(SAS),
∴CE=BD,∠B=∠ACE,
∴∠ACB+∠ACE=90°,即CE⊥BD;
(2)当∠ACB=45°时,CE⊥BD(如图2).
理由:过点A作AG⊥AC交CB的延长线于点G,
则∠GAC=90°,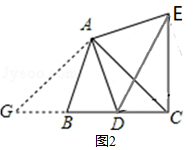
∵∠ACB=45°,∠AGC=90°-∠ACB,
∴∠AGC=90°-45°=45°,
∴∠ACB=∠AGC=45°,
∴AC=AG,…(8分)
在△GAD与△CAE中,
$\left\{\begin{array}{l}{AC=AG}\\{∠DAG=∠EAC}\\{AD=AE}\end{array}\right.$
∴△GAD≌△CAE(SAS),
∴∠ACE=∠AGC=45°,
∠BCE=∠ACB+∠ACE=45°+45°=90°,即CE⊥BC.
点评 此题为三角形综合题,主要考查了全等三角形的判定与性质及等腰直角三角形的性质,解决问题的关键是作辅助线构造全等三角形,根据全等三角形的对应边相等,对应角相等进行求解.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:解答题
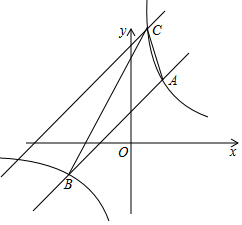 如图,在平面直角坐标系中,直线y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于点A(2,m)、B(-4,-2),其中k1≠0,k2>0.
如图,在平面直角坐标系中,直线y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象分别交于点A(2,m)、B(-4,-2),其中k1≠0,k2>0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由②③,得④ | B. | 由①③,得⑤ | C. | 由①②,得⑥ | D. | 由①④,得⑥ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将一副三角尺拼成如图所示,∠BAC=45°,∠D=30°,∠BCA=∠DCE=90°,过点C作CF∥AB,交DE于点F,则∠EFC=75度.
将一副三角尺拼成如图所示,∠BAC=45°,∠D=30°,∠BCA=∠DCE=90°,过点C作CF∥AB,交DE于点F,则∠EFC=75度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
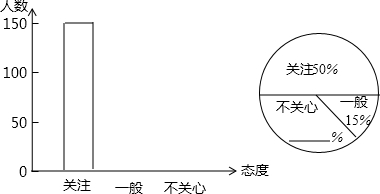 为了了解市民对“汕头市创建全国文明城市”的态度,某一天,小明等同学在本市的甲、乙和丙三个村的村民进行了一次随机调査,结果如图表:
为了了解市民对“汕头市创建全国文明城市”的态度,某一天,小明等同学在本市的甲、乙和丙三个村的村民进行了一次随机调査,结果如图表:| 村民态度 | 甲村 | 乙村 | 丙村 | 合计 |
| 关注 | 20 | 75 | 55 | 150 |
| 一般 | 23 | 5 | 17 | 45 |
| 不关心 | 57 | 20 | 28 | 105 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-3 | B. | -4<a<-3 | C. | -4≤a<-3 | D. | -4<a≤-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
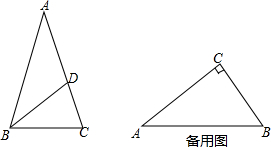 我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.
我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“內似线”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com