
| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 6 | D. | 3 |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
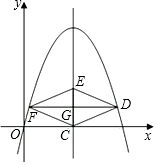 如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.
如图,在平面直角坐标系中,抛物线y=-x2+bx经过点A(4,0).直线x=2与x轴交于点C,点E是直线x=2上的一个动点,过线段CE的中点G作DF⊥CE交抛物线于D、F两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
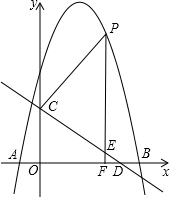 如图,抛物线y=ax2+bx+5与x轴交于A(-1,0)、B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是抛物线上一动点,过点P作直线PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
如图,抛物线y=ax2+bx+5与x轴交于A(-1,0)、B(5,0)两点,直线y=-$\frac{3}{4}$x+3与y轴交于点C,与x轴交于点D.点P是抛物线上一动点,过点P作直线PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;(2)CF=CD;(3)AC+CD=AB;(4)BE=CF;(5)BF=2BE,其中正确的结论个数是( )
如图,在Rt△ABC中,AC=BC,∠ACB=90°,AD平分∠BAC,BE⊥AD交AC的延长线于F,E为垂足.则结论:(1)AD=BF;(2)CF=CD;(3)AC+CD=AB;(4)BE=CF;(5)BF=2BE,其中正确的结论个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
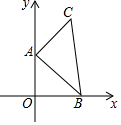 如图所示,点A的坐标为(0,1),点B是x轴上位于原点右侧的一个动点,以AB为直角边作Rt△ABC,使tan∠ABC=$\frac{3}{4}$,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图所示,点A的坐标为(0,1),点B是x轴上位于原点右侧的一个动点,以AB为直角边作Rt△ABC,使tan∠ABC=$\frac{3}{4}$,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )| A. | 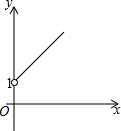 | B. | 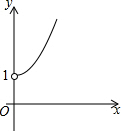 | C. | 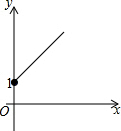 | D. | 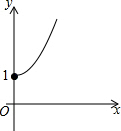 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?画树状图或列表说明理由.
用如图所示的A,B两个转盘进行“配紫色”游戏(红色和蓝色在一起配成了紫色).小亮和小刚同时转动两个转盘,若配成紫色,小亮获胜,否则小刚获胜.这个游戏对双方公平吗?画树状图或列表说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com