练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图，已知：四边形ABCD是正方形，点E、F在对角线BD上，且BF=DE．
    求证：AE=CF．

    分析 欲证明AE=CF，只要证明△ABE≌△CDF即可．

    解答 证明：∵四边形ABCD是正方形，
    ∴AB=CD，AB∥CD，
    ∴∠ABD=∠BDC，
    ∵BF=DE，
    ∴BE=DC，
    在△ABE 和△CDF中，
    $\left\{\begin{array}{l}{AB=CD}\\{∠ABE=∠CDF}\\{BE=DF}\end{array}\right.$，
    ∴△ABE≌△CDF，
    ∴AE=CF．

    点评 本题考查正方形的性质、全等三角形的判定和性质等知识，解题的关键是灵活应用这些知识解决问题，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．如图，点A，B在由若干个边长为1个单位长度的小正方形组成的网格图中，已知点A的坐标为（-1，0），点B的坐标为（1，4），点C在x轴上，且AC=2．．
    （1）请在图中找出x轴、y轴及原点O；
    （2）求点C的坐标，并画出△ABC；
    （3）将△ABC的各顶点的横坐标和纵坐标相乘$\frac{1}{2}$，得到△A1B1C1，求B1C1的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知正方形ABCD对角线AC、BD相交于点O，且AC=16cm，则BO=8cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．哈尔滨透龙山的门票价格如表所示：
    购票人数1～50人51～100人100人以上
    票   价15元/人13元/人10元/人
    我校九年级甲、乙两个班共100多人去透龙山举行毕业联欢活动，其中甲班有50多人，乙班不足50人，如果以班为单位分别买门票，两个班一共应付1435元；如果两个班联合起来作为一个团体购票，一共要付1030元，问甲、乙两班分别有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

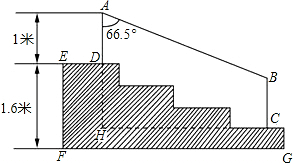    13．某商场门前的台阶截面如图中阴影部分所示，已知台阶有四级小台阶且每一级小台阶高度相等，台阶高度EF为1.6米，现要做一个不锈钢的扶手AB及两根与FG垂直且长度均为1米的不锈钢架杆AD和BC（杆子的低端分别为D，C），且∠DAB=66.5°（cos66.5°≈0.4）．
    （1）求点D与点C的高度差DH；
    （2）求所用不锈钢材料的总长度（即AD+AB+BC的长）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）计算：$\sqrt{12}$-2cos30°+（$\sqrt{3}$-1）0-（$\frac{1}{8}$）-1
    （2）解不等式：$\frac{3-x}{2}$-（x-1）≤$\frac{5+x}{4}$，并把它的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．写出一个二次根式使得它与$\sqrt{3}$为同类二次根式，这个二次根式可以是2$\sqrt{3}$；写出一个最简二次根式，使得它大于2小于4，这个二次根式可以是$\sqrt{7}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．当x=-2时，分式$\frac{{{x^2}-4}}{x+2}$无意义．若分式$\frac{|a|-2}{{（{a-2}）（{a+3}）}}$的值为0，则a=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图，BC为⊙O的直径，DE为⊙O的切线，CA与弦BE的延长线交于点A，D为AC的中点．
    （1）求证：AC为⊙O的切线；
    （2）若DE=3，tanB=$\frac{1}{3}$，求⊙O的半径．

    查看答案和解析>>

    同步练习册答案