
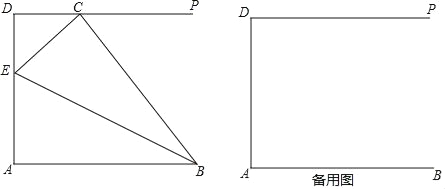
【题目】如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).
(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;
(2)当△ABE与△BCE相似时,求线段CD的长;
(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.
【答案】(1)16(2)当△ABE∽△EBC时,线段CD的长为2或![]() (3)
(3)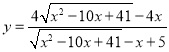 (0<x<4.1)
(0<x<4.1)
【解析】试题分析:(1) 过C作CH⊥AB与H,由∠A=90°,DP∥AB,可得得四边形ADCH为矩形,在△BCH中,CH=AD=4,∠BHC=90°,tan∠CBH=2,得HB=CH÷2=2, 所以CD=AH=5-2=3,
则四边形ABCD的面积=![]() ,
,
(2) 由BE平分∠ABC,得∠ABE=∠EBC,当△ABE∽△EBC时,
∠BCE=∠BAE=90°,由BE=BE,得△BEC≌△BEA,得BC=BA=5,在△BCH中,BH=![]() ,所以CD=AH=5-3=2.
,所以CD=AH=5-3=2.
∠BEC=∠BAE=90°,延长CE交BA延长线于T,由∠ABE=∠EBC,
∠BEC=∠BET=90°,BE=BE,得△BEC≌△BET,得BC=BT,且CE=TE,又CD∥AT,得AT=CD.令CD=x,则在△BCH中,BC=BT=5+x,BH=5-x,∠BHC=90°,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
(3) 延长BE交CD延长线于M,因为AB∥CD,所以∠M=∠ABE=∠CBM,所以CM=CB,
在△BCH中,由勾股定理可得: ![]() ,
,
则DM=CM-CD= ![]() ,又因为DM∥AB,可得
,又因为DM∥AB,可得![]() ,即
,即![]() ,
,
即可得到: 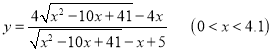 .
.
试题解析:(1)过C作CH⊥AB与H,
由∠A=90°,DP∥AB,得四边形ADCH为矩形,
在△BCH中,CH=AD=4,∠BHC=90°,tan∠CBH=2,得HB=CH÷2=2,
所以CD=AH=5-2=3,
则四边形ABCD的面积=![]() ,
,
(2)由BE平分∠ABC,得∠ABE=∠EBC,
当△ABE∽△EBC时,
∠BCE=∠BAE=90°,由BE=BE,得△BEC≌△BEA,得BC=BA=5,
于是在△BCH中,BH=![]() ,
,
所以CD=AH=5-3=2.
∠BEC=∠BAE=90°,延长CE交BA延长线于T,
由∠ABE=∠EBC,∠BEC=∠BET=90°,BE=BE,得△BEC≌△BET,得BC=BT,
且CE=TE,又CD∥AT,得AT=CD.
令CD=x,则在△BCH中,BC=BT=5+x,BH=5-x,∠BHC=90°,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
综上,当△ABE∽△EBC时,线段CD的长为2或![]() .
.
(3)延长BE交CD延长线于M,
由AB∥CD,得∠M=∠ABE=∠CBM,所以CM=CB,
在△BCH中, ![]() ,
,
则DM=CM-CD= ![]() ,
,
又DM∥AB,得![]() ,即
,即![]() ,
,
解得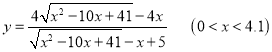 .
.


 同步轻松练习系列答案
同步轻松练习系列答案科目:初中数学 来源: 题型:
【题目】如图(1),AB=4![]() ,AC⊥AB,BD⊥AB,AC=BD=3
,AC⊥AB,BD⊥AB,AC=BD=3![]() .点 P 在线段 AB 上以 1
.点 P 在线段 AB 上以 1![]() 的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为
的速度由点 A 向点 B 运动,同时,点 Q 在线段 BD 上由点 B 向点 D 运动.它们运动的时间为 ![]() (s).
(s).
(1)若点 Q 的运动速度与点 P 的运动速度相等,当![]() =1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;
=1 时,△ACP 与△BPQ 是否全等,请说明理由, 并判断此时线段 PC 和线段 PQ 的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点 Q 的运动速度为![]()
![]() ,是否存在实数
,是否存在实数![]() ,使得△ACP 与△BPQ 全等?若存在,求出相应的
,使得△ACP 与△BPQ 全等?若存在,求出相应的![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
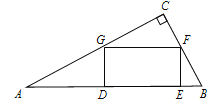
【题目】如图,在Rt△ABC中,∠C=90°,矩形DEFG的顶点G、F分别在AC、BC上,DE在AB上.
(1)求证:△ADG∽△FEB;
(2)若AG=5,AD=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
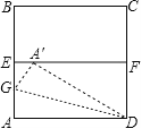
【题目】如图,ABCD是一张边长为4cm的正方形纸片,E,F分别为AB,CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上的点A′处折痕交AE于点G,则∠ADG=____°EG=___cm .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列4个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是( )
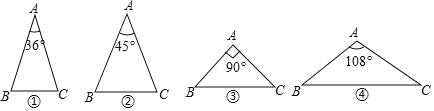
A. ①③B. ①②④C. ①③④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点![]() 的“
的“![]() 值”定义如下:若点
值”定义如下:若点![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 长度的最大值与最小值之差即为点
长度的最大值与最小值之差即为点![]() 的“
的“![]() 值”,记为
值”,记为![]() .特别的,当点
.特别的,当点![]() ,
, ![]() 重合时,线段
重合时,线段![]() 的长度为0.
的长度为0.
当⊙![]() 的半径为2时:
的半径为2时:
(1)若点![]() ,
, ![]() ,则
,则![]() _________,
_________, ![]() _________;
_________;
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求出点
,求出点![]() 的横坐标;
的横坐标;
(3)直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点
轴分别交于点![]() ,
, ![]() .若线段
.若线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请你直接写出
,请你直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com