
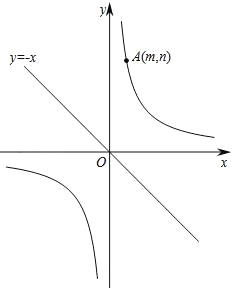
【题目】如图,已知直线y=﹣x和双曲线![]() (k>0),点A(m,n)(m>0)在双曲线
(k>0),点A(m,n)(m>0)在双曲线![]() 上.
上.
(1)当m=n=2时,
①直接写出k的值;
②将直线y=﹣x作怎样的平移能使平移后的直线与双曲线![]() 只有一个交点.
只有一个交点.
(2)将直线y=﹣x绕着原点O旋转,设旋转后的直线与双曲线![]() 交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:
交于点B(a,b)(a>0,b>0)和点C.设直线AB,AC分别与x轴交于D,E两点,试问:![]() 与
与![]() 的值存在怎样的数量关系?请说明理由.
的值存在怎样的数量关系?请说明理由.
【答案】(1)①k=4;②只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点;(2)综上所述,![]() .理由见试题解析.
.理由见试题解析.
【解析】
试题分析:(1)①当m=n=2时,得出A(2,2),把点A(2,2)代入双曲线![]() (k>0)求出k的值即可;
(k>0)求出k的值即可;
②设平移后的直线解析式为y=﹣x+b1,由直线和双曲线解析式组成方程组,整理可得方程:x2﹣b1x+4=0,当判别式=0时,求出b1=±4即可;
(2)分两种情况讨论:由双曲线的对称性可知,C(﹣a,﹣b),①当点A在直线BC的上方时,过A、B、C分别作y轴的垂线,垂足分别为F、G、H,则OF=n,OG=OH=b,得出FG=OF﹣OG=n﹣b,FH=OF+OH=n+b,由平行线得出比例式,即可得出结论;
②当点A在直线BC的下方时,同理可得出结论;即可得出结果.
试题解析:(1)①当m=n=2时,A(2,2),
把点A(2,2)代入双曲线![]() (k>0)得:k=2×2=4;
(k>0)得:k=2×2=4;
②设平移后的直线解析式为y=﹣x+b1,由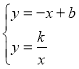 可得,
可得,![]() ,
,
整理可得:x2﹣b1x+4=0,当△=![]() -4×1×4=0,即b1=±4时,方程x2﹣b1x+4=0有两个相等的实数根,此时直线y=﹣x+b1与双曲线只有一个交点,∴只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点;
-4×1×4=0,即b1=±4时,方程x2﹣b1x+4=0有两个相等的实数根,此时直线y=﹣x+b1与双曲线只有一个交点,∴只要将直线y=﹣x向上或向下平移4个单位长度,所得到的直线与双曲线只有一个交点;
(2)![]() =2,理由如下:
=2,理由如下:
分两种情况讨论:由双曲线的对称性可知,C(﹣a,﹣b)
①当点A在直线BC的上方时,如图所示:过A、B、C分别作y轴的垂线,垂足分别为F、G、H,
则OF=n,OG=OH=b,∴FG=OF﹣OG=n﹣b,FH=OF+OH=n+b,
∵AF∥BG∥x轴,∴![]() ,∵AF∥x轴∥CH,
,∵AF∥x轴∥CH,
∴![]() ,∴
,∴![]() =2;
=2;
②当点A在直线BC的下方时,
同理可求:![]() ,
, ![]() ,
,
∴![]() ;
;
综上所述,![]() .
.


科目:初中数学 来源: 题型:
【题目】广州市运动员在最近八届亚运会上获得金牌的运动项目种类及金牌数量如下表所示:
田径 | 羽毛球 | 篮球 | 水球 | 网球 | 台球 | 足球 | 体操 | 游泳 | 举重 | 射击 | 击剑 | 拳击 | 赛艇 | 跳水 |
7 | 8 | 2 | 4 | 2 | 1 | 1 | 3 | 2 | 4 | 4 | 12 | 1 | 5 | 1 |
给出下列说法:①广州市运动员在最近八届亚运会上获得金牌的运动项目共有15个;②广州市运动员在最近八届亚运会上获得金牌的总数是57;③上表中,击剑类的频率约为0.211.其中正确的有( )
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )

A. 100° B. 80° C. 70° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】好久未见的A,B,C,D,E五位同学欢聚一堂,他们相互握手一次,中途统计各位同学握手次数为:A同学握手4次,B同学握手3次,C同学握手2次,D同学握手1次,那么此时E同学握手 次.
查看答案和解析>>
科目:初中数学 来源: 题型:
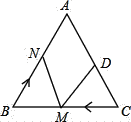
【题目】如图,在等边△ABC中,AB=AC=BC=10厘米,DC=4厘米.如果点M以3厘米/秒的速度运动.
(1)如果点M在线段CB上由点C向点B运动,点N在线段BA上由B点向A点运动.它们同时出发,若点N的运动速度与点M的运动速度相等.
①经过2秒后,△BMN和△CDM是否全等?请说明理由.
②当两点的运动时间为多少时,△BMN是一个直角三角形?
(2)若点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,都顺时针沿△ABC三边运动,经过25秒点M与点N第一次相遇,则点N的运动速度是 厘米/秒.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
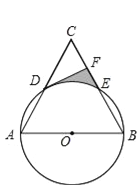
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com