
【题目】如图,已知:∠C=∠D,OD=OC.求证:DE=CE.

【答案】证明见解析
【解析】试题分析:利用ASA证明△OBC≌△OAD,根据全等三角形的对应边相等可得OA=OB,再由OD=OC,即可得AC=BD,根据AAS证明△ACE≌△BDE,再由全等三角形的对应边相等即可得结论.
试题解析:
在△OBC和△OAD中,
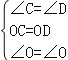 ,
,
∴△OBC≌△OAD(ASA),
∴OA=OB,
∵OD=OC,
∴OD﹣OB=OC﹣OA,即AC=BD,
在△ACE和△BDE中,
 ,
,
∴△ACE≌△BDE(AAS),
∴DE=CE.
【题型】解答题
【结束】
27
【题目】如图,以等腰直角三角形ABC的斜边AB为边向内作等边△ABD,连接DC,以DC为边,作等边△DCE,点B、E在CD的同侧.
(1)求∠BCE的大小;
(2)求证:BE=AC.

【答案】(1)75°(2)证明见解析
【解析】试题分析:(1)根据已知条件易证△ADC≌△BDE,根据全等三角形的性质可得BE=AC=BC,∠EBD=∠CAD=15°,根据等腰三角形的性质和三角形的内角和定理即可求得∠BCE的大小;(2)由(1)中的△ADC≌△BDE,根据全等三角形的对应边相等即可得结论.
试题解析:
(1)∵△ACB是等腰直角三角形,
∴AC=BC,∠CAB=∠CBA=45°
∵△ABD和△DEC是等边三角形,
∴AD=BD,CD=DE,∠ADB=∠EDC=60°,∠DAB=∠DBA=60°
∴∠DAC=60°﹣45°=15°,∠DBC=15°,∠EDB=∠CDA=60°﹣∠BCD,
在△ADC和△BDE中
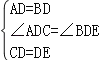
∴△ADC≌△BDE,
∴BE=AC=BC,∠EBD=∠CAD=15°,
∴∠BCE=∠BEC=![]() (180°﹣15°﹣15°)=75°;
(180°﹣15°﹣15°)=75°;
(2)证明:∵△ADC≌△BDE,
∴BE=AC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若x、y是有理数,设N=3x2+2y2﹣18x+8y+35,则N( )
A. 一定是负数 B. 一定不是负数 C. 一定是正数 D. N的取值与x、y的取值有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求代数式的值: ![]() ,其中m=1.
,其中m=1.
【答案】(1) ![]() ,
, ![]()
【解析】先进行分式的混合运算,再代入求值即可.
解:原式= ,
,
= ,
,
=![]() ;
;
当m =1时,原式=![]() =-
=-![]() .
.
【题型】解答题
【结束】
25
【题目】如图,在△ABC中,D为BC边的中点,过D点分别作DE∥AB交AC于点E,DF∥AC交AB于点F.
求证:BF=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知⊙O上依次有A、B、C、D四个点,![]() =
=![]() ,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
,连接AB、AD、BD,弦AB不经过圆心O,延长AB到E,使BE=AB,连接EC,F是EC的中点,连接BF.
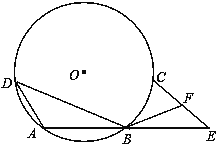
(1)求证:BF=![]() BD;
BD;
(2)设G是BD的中点,探索:在⊙O上是否存在点P(不同于点B),使得PG=PF?并说明PB与AE的位置关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某商品的进价为每件30元,九(1)班数学兴趣小组经过市场调查,整理出该商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
第x天 | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)分别求出第25天和第60天商家在销售该商品时所获得的利润;
(2)问销售该商品第几天时,当天的销售利润为6050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
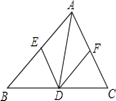
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com