
| A. | 2.4×107 | B. | 24×107 | C. | 24×109 | D. | 2.4×108 |
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
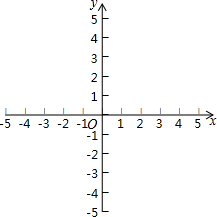 我们已经知道y=ax2+c的图象可以由函数y=ax2通过上、下平侈所得,例如,函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2的图象通过向下平移2个单位长度而得到,那么函数y=$\frac{1}{2}$(x-2)2的图象是否可由函数y=$\frac{1}{2}$x2的图象平移而得到呢?请在图中试一试,你能从中发现什么规律吗?
我们已经知道y=ax2+c的图象可以由函数y=ax2通过上、下平侈所得,例如,函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2-2的图象可以由函数y=$\frac{1}{2}$x2的图象通过向下平移2个单位长度而得到,那么函数y=$\frac{1}{2}$(x-2)2的图象是否可由函数y=$\frac{1}{2}$x2的图象平移而得到呢?请在图中试一试,你能从中发现什么规律吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
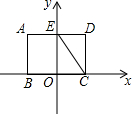 以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.
以矩形ABCD的边BC的中点O为原点,建立如图所示的平面直角坐标系,边AD交y轴于点E,连接CE.已知OC、OE的长是关于x的一元二次方程x2-5x+6=0的两个根,且OC<OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,AB是直径,CD是⊙O上的点,E为AB延长线上一点,连接OC,CD,DE,满足∠OCD=45°且OC∥DE.
如图,在⊙O中,AB是直径,CD是⊙O上的点,E为AB延长线上一点,连接OC,CD,DE,满足∠OCD=45°且OC∥DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
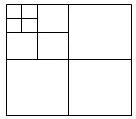 如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…
如下图,将一张正方形纸片,第一次剪成四个大小形状一样的正方形,第二次再将其中的一个正方形,再按同样的方法,剪成四个小正方形,如此循环进行下去…| 剪的次数 | 1 | 2 | 3 | 4 | … |
| 正方形个数 | 4 | 7 | 10 | 13 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 高度变化 | 记作 |
| 上升4.4km | 4.4km |
| 下降3.2km | -3.2km |
| 上升1.1km | +1.1km |
| 下降1.5km | -1.5km |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com