
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

科目:初中数学 来源: 题型:
【题目】如图,二次函数y=―ax2+2ax+c(a>0)的图象交x轴于A、B两点,交y轴于点C,过A的直线y=kx+2k(k≠0)与这个二次函数图象交于另一点F,与其对称轴交于点E,与y轴交于点D,且DE=EF.
(1)求A点坐标;
(2)若△BDF的面积为12,求此二次函数的表达式;
(3)设二次函数图象顶点为P,连接PF,PC,若∠CPF=2∠DAB,求此二次函数的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
经过社团成员讨论发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() 就可以解决问题(如图
就可以解决问题(如图![]() .
.
请回答:![]()
![]() ,
,![]() .
.
(2)请参考以上解决思路,解决问题:
如图3,在四边形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
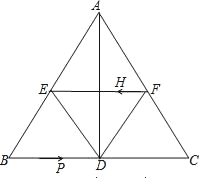
【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,E点F点分别为AB,AC的中点.
(1)求证:四边形AEDF是菱形;
(2)求菱形AEDF的面积;
(3)若H从F点出发,在线段FE上以每秒2cm的速度向E点运动,点P从B点出发,在线段BC上以每秒3cm的速度向C点运动,问当t为何值时,四边形BPHE是平行四边形?当t取何值时,四边形PCFH是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(3分)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD∶GC∶EB的结果(不必写计算过程);
(2)(3分)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD∶GC∶EB;
(3)(2分)把图(2)中的正方形都换成矩形,如图(3),且已知DA∶AB=HA∶AE=m: n,此时HD∶GC∶EB的值与(2)小题的结果相比有变化吗?如果有变化,直接写出变化后的结果(不必写计算过程).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A,O,B依次在直线MN上.将射线OA绕点O沿顺时针方向以每秒18°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒6°的速度旋转(如图2).设旋转时间为t(0≤t≤30,单位秒).
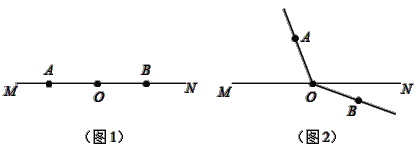
(1)当t=10时,∠AOB= °;
(2)在旋转过程中是否存在这样的t,使得射线OM是由射线OB、射线OA组成的角(指大于0°而不超过180°的角)的平分线?如果存在,请求出t的值;如果不存在,请说明理由.
(3)在运动过程中,当∠AOB=45°时,求t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com