
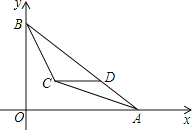
【题目】如图,平面直角坐标系中,A(8,0),B(0,6),∠BAO,∠ABO的平分线相交于点C,过点C作CD∥x轴交AB于点D,则点D的坐标为( )
A.( ![]() ,2)B.(
,2)B.( ![]() ,1)C.(
,1)C.( ![]() ,2)D.(
,2)D.(![]() ,1)
,1)
【答案】A
【解析】
延长DC交y轴于F,过C作CG⊥OA于G,CE⊥AB于E,根据角平分线的性质得到FC=CG=CE,求得DH=CG=CF,设DH=3x,AH=4x,根据勾股定理得到AD=5x,根据平行线的性质得到∠DCA=∠CAG,求得∠DCA=∠DAC,得到CD=HG=AD=5x,列方程即可得到结论.
解:延长DC交y轴于F,过C作CG⊥OA于G,CE⊥AB于E,
∵CD∥x轴,
∴DF⊥OB,
∵∠BAO,∠ABO的平分线相交于点C,
∴FC=CG=CE,
∴DH=CG=CF,
∵A(8,0),B(0,6),
∴OA=8,OB=6,
∴tan∠OAB=![]() =
=![]() =
=![]() ,
,
∴设DH=3x,AH=4x,
∴AD=5x,
∵CD∥OA,
∴∠DCA=∠CAG,
∵∠DAC=∠GAC,
∴∠DCA=∠DAC,
∴CD=HG=AD=5x,
∴3x+5x+4x=8,
∴x=![]() ,
,
∴DH=2,OH=![]() ,
,
∴D(![]() ,2),
,2),
故选:A.



 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】中华人民共和国《城市道路路内停车泊位设置规范》规定:
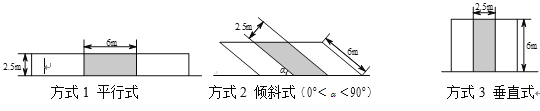
一、在城市道路范围内,在不影响行人、车辆通行的情况下,政府有关部门可以规划停车泊位.停车泊位的排列方式有三种,如图所示:
二、双向通行道路,路幅宽![]() 米以上的,可在两侧设停车泊位,路幅宽
米以上的,可在两侧设停车泊位,路幅宽![]() 米到
米到![]() 米的,可在单侧设停车泊位,路幅宽
米的,可在单侧设停车泊位,路幅宽![]() 米以下的,不能设停车泊位;
米以下的,不能设停车泊位;
三、规定小型停车泊位,车位长![]() 米,车位宽
米,车位宽![]() 米;
米;
四、设置城市道路路内机动车停车泊位后,用于单向通行的道路宽度应不小于![]() 米.
米.
根据上述的规定,在不考虑车位间隔线和车道间隔线的宽度的情况下,如果在一条路幅宽为![]() 米的双向通行车道设置同一种排列方式的小型停车泊位,请回答下列问题:
米的双向通行车道设置同一种排列方式的小型停车泊位,请回答下列问题:
(1)可在该道路两侧设置停车泊位的排列方式为 ;
(2)如果这段道路长![]() 米,那么在道路两侧最多可以设置停车泊位 个.
米,那么在道路两侧最多可以设置停车泊位 个.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
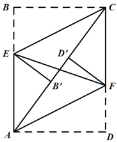
【题目】如图,在矩形ABCD中,点E、F分别在AB、CD边上,AD=6,AB=8,将△CBE沿CE翻折,使B点的对应点B′刚好落在对角线AC上,将△ADF沿AF翻折,使D点的对应点D′也恰好落在对角线AC上,连接EF,则EF的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的解析式为
的解析式为![]() ,则下列说法中错误的是( )
,则下列说法中错误的是( )
A.![]() 确定抛物线的开口方向与大小
确定抛物线的开口方向与大小
B.若将抛物线![]() 沿
沿![]() 轴平移,则
轴平移,则![]() ,
,![]() 的值不变
的值不变
C.若将抛物线![]() 沿
沿![]() 轴平移,则
轴平移,则![]() 的值不变
的值不变
D.若将抛物线![]() 沿直线
沿直线![]() :
:![]() 平移,则
平移,则![]() 、
、![]() 、
、![]() 的值全变
的值全变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
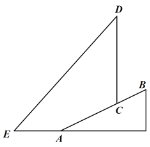
【题目】为践行“绿水青山就是金山银山”的重要思想,某森林保护区开展了寻找古树活动.如图,在一个坡度(或坡比)i=1:2.4的山坡AB上发现有一棵古树CD.测得古树底端C到山脚点A的距离AC=26米,在距山脚点A水平距离6米的点E处,测得古树顶端D的仰角∠AED=48°(古树CD与山坡AB的剖面、点E在同一平面上,古树CD与直线AE垂直),则古树CD的高度约为多少米?(参考数据:sin48°≈0.73,cos48°≈0.67,tan48°≈1.11)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将
将![]() 折叠,得
折叠,得![]() .
.
(1)如图所示,当![]() 时,
时,![]() _______度;
_______度;

(2)如图所示,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 为
为![]() 中点时,点
中点时,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,将
重合的一个动点,将![]() 沿
沿![]() 折叠,得到
折叠,得到![]() ,连接
,连接![]() ,求
,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十九大召开后,某社区开展了“市民对十九大的关注情况”调查,采用随机抽样的方法访问了部分年龄在18周岁以上的城乡居民.小聪根据调查数据绘制了如下不完整的频数分布置表和扇形统计图.请根据图表解答下列问题.
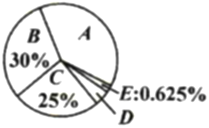
关注情况 | 频数 |
非常关注( | 128 |
比较关注( | |
一般关注( | 80 |
不太关注( | |
不关注( | 2 |
(1)请完成频数分布表空格数据填写;
(2)求“非常关注”部分扇形圆心角的度数;
(3)若该社区18周岁以上居民共有20000人,请估计“比较关注”和“非常关注”的居民共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形网格中,每个小正方形的边长均为1,
的正方形网格中,每个小正方形的边长均为1,![]() 的三个顶点均在小正方形的顶点上.
的三个顶点均在小正方形的顶点上.
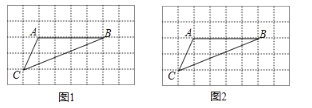
(1)在图1中画一个![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是轴对称图形;
为顶点的四边形是轴对称图形;
(2)在图2中画![]() (点
(点![]() 在小正方形的顶点上),使
在小正方形的顶点上),使![]() 的周长等于
的周长等于![]() 的周长,且以
的周长,且以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是中心对称图形;
为顶点的四边形是中心对称图形;
(3)直接写出图2中四边形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com