

���� ��1����C��CM��DG����DG���ӳ����ڵ�M����֤����CDM�ա�ABE���������߶εĺͲ����ý��ۣ�
��2����D��DN��CF����CF�ڵ�N����֤����CDN�ա�BAE���������߶εĺͲ����ý��ۣ�
��3����C��CH��DG��H����֤����CDH�ա�ABE���������߶εĺͲ����ý��ۣ�
��� �⣺
��1����ͼ1����C��CM��DG����DG���ӳ����ڵ�M��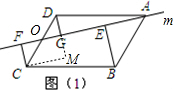
��DM��CM��CF��AF��CM��DG��
���DMC=��CFG=��AEB=90�㣬
���ı���GFCMΪ���Σ�
��FG��CM��FC=GM��
���ı���ABCDΪƽ���ı��Σ�
��CD=AB��CD��AB��
���DOG=��BAE=��DCM��
�ڡ�CDM�͡�ABE��
$\left\{\begin{array}{l}{��DCM=��ABE}\\{��DMC=��BEA}\\{CD=AB}\end{array}\right.$
���CDM�ա�ABE��AAS����
��DM=BE��
��BE=DG+GM=CF+DG��
�ʴ�Ϊ��BE=CF+DG��
��2����ͼ2����D��DN��CF����CF�ڵ�N���ӳ�CD��AF�ڵ�P��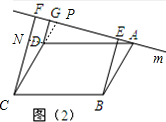
��DG��AF��CF��AF��
���ı���DGFNΪ���Σ�
��ND��AF����DG=NF��
���ı���ABCDΪƽ���ı��Σ�
��AB=CD����AB��CD��
���CDN=��DPG=��BAE��
�ڡ�CDN�͡�BAE��
$\left\{\begin{array}{l}{��CDN=��BAE}\\{��CND=��BEA}\\{CD=AB}\end{array}\right.$
���CDN�ա�BAE��AAS����
��CN=BE��
��CF=CN+DF=BE+DG��
�ʴ�Ϊ��CF=BE+DG��
��3�����룺DG=BE+CF��
֤������ͼ3����C��CH��DG��H��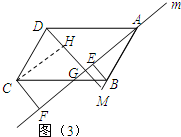
�֡�CF��m��DG��m��
���ı���CFGH�Ǿ��Σ�
��CF=HG��
��DG��m��BE��m��
���DGE=��BEG=90�㣬
��DG��BE��
���ABE=��AMG
�ߡ�ABCD��
��AD��BC��CD=AB��
���CDH=��AMG��
���CDH=��ABE��
�ڡ�CDH�͡�ABE��
$\left\{\begin{array}{l}{��CDH=��ABE}\\{��DHC=��AEB}\\{CD=AB}\end{array}\right.$
���CDH�ա�ABE��AAS����
��DH=BE��
��DG=DH+HG=BE+CF��
��DG=BE+CF��
���� ����Ϊ�ı��ε��ۺ�Ӧ�ã��漰֪ʶ����ƽ���ı��ε����ʡ����ε��ж������ʡ�ȫ�������ε��ж������ʵȣ�����������ȫ���ǽ���Ĺؼ���ע�������߶εĺͲ��ϵ�����⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�


 �������ͬ������ϵ�д�
�������ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B�� | 2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$ | C�� | $\sqrt{��-4������-9��}$=$\sqrt{-4}$��$\sqrt{-9}$ | D�� | $\sqrt{6}$��$\sqrt{3}$=$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com