
 如图,在平面直角坐标系中,点A(0,8),点B(12,8),点C(18,0),连接AB,BC.
如图,在平面直角坐标系中,点A(0,8),点B(12,8),点C(18,0),连接AB,BC.分析 分析:(1)当纵坐标相等时,直线与x轴平行;
(2)由于AB∥OC,当BM=CN时,四边形MBCN为平行四边形.用含x(或t)的代数式分别表示出BM、CN,得到关于x(或t)的方程,求出x的值;
(3)分别过点B、M作BD⊥OC于D,ME⊥OC于E,用含x的代数式表示出NE,通过勾股定理得到关于x的一元二次方程,求出x.
解答 解:(1)∵A(0,8),B(12,8),由于其纵坐标相等,
∴AB∥x轴,即AB与OC平行.
故答案为:平行;
(2)由题意知,CN=OC-ON=18-x=2AM,
∴AM=9-$\frac{x}{2}$,
∴MB=AB-AM=12-(9-$\frac{x}{2}$)=3+$\frac{x}{2}$,
∵AB∥OC,
∴当MB=CN时,四边形MBCN为平行四边形,即3+$\frac{x}{2}$=18-x,
解得:x=10,
∴当x=10时,四边形MBCN为平行四边形;
(3)过B作BD⊥OC于D,则BD=AO=8,DC=OC-OD=18-12=6,
∴BC2=BD2+DC2=82+62=100,
过M作ME⊥OC于E,则ME=AO=8,EN=ON-OE=ON-AM=x-(9-$\frac{x}{2}$)=$\frac{3x}{2}$-9,
∴MN2=EM2+EN2=82+($\frac{3x}{2}$-9)2,
由MN2=BC2得:82+($\frac{3x}{2}$-9)2=102,解得:x1=10,x2=2.
在(2)的条件下,当x=10或者2时,满足MN=BC.
点评 点评:本题是一道动点类题目,主要考察了平行四边形的判定、说明线段位置、数量关系的方法.由于DC的长等于6是恒定的,BD=ME=AO,解决(3)也可以用分类讨论的办法.当点N在点E右边时,$\frac{3x}{2}$-9=6,解得,x=10;当点N在点E左边时,EN=AM-OE=9-$\frac{x}{2}$-x=9-$\frac{3x}{2}$,即9-$\frac{3x}{2}$=6,解得x=2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -2x+1 | D. | 2x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
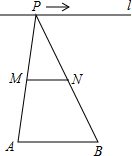 如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )
如图,点A,B为定点,定直线l∥AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:①线段MN的长;②△PAB的周长;③△PMN的面积;④∠APB的大小.其中随点P的移动不会变化的是( )| A. | ①② | B. | ②④ | C. | ①③ | D. | ①④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )
如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
七(1)班同学为了解某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 12% |
| 5<x≤10 | 12 | 24% |
| 10<x≤15 | 16 | 32% |
| 15<x≤20 | 10 | 20% |
| 20<x≤25 | 4 | 8% |
| 25<x≤30 | 2 | 4% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com