
【题目】某商场将每台进价为3000元的彩电以3900元的销售价售出,每天可销售出6台.这种品牌的彩电每台降价100x(x为整数)元,每天可以多销售出3x台.
(1)降价后:每台彩电的利润是______元,每天销售彩电______台,设商场每天销售这种彩电获得的利润为y元,试写出y与x之间的函数关系式,并写出x的取值范围(保证商家不亏本);
(2)销售该品牌彩电每天获得的最大利润是多少?此时,每台彩电的销售价是多少时,彩电的销售量和营业额均较高?
【答案】(1)![]() ;
;![]() ;
;![]() ;
;![]() ;(2)销售该品牌彩电每天获得的最大利润是9000元,每台彩电的销售价是3000元时,彩电的销售量和营业额较高.
;(2)销售该品牌彩电每天获得的最大利润是9000元,每台彩电的销售价是3000元时,彩电的销售量和营业额较高.
【解析】
(1)由题目知每台彩电的利润是(3900-100x-3000)元,则y=(3900-100x-3000)(6+3x),然后化简即可;
(2)用配方法化简y与x的函数关系式,根据二次函数的性质即可得到结论;然后得出x的值,相比较下得出w的值.
(1)由题意得:每台彩电的利润是![]() 元,每天销售
元,每天销售![]() 台,
台,
则![]()
![]() ;
;![]() .
.
故答案为:![]() ,
,![]() ;
;
(2)![]() .
.
当![]() 或4时,
或4时,![]() 最大值
最大值![]() .
.
设每台彩电的销售价是![]() 时,彩电的销售量为
时,彩电的销售量为![]() ,营业额为
,营业额为![]() ,
,
根据题意得,![]() ,
,
∵![]() 为整数,
为整数,
∴当![]() 时,彩电单价为3000元,每天销售33台,营业额为
时,彩电单价为3000元,每天销售33台,营业额为![]() 元,
元,
当![]() 时,彩电单价为3100元,每天销售30台,营业额为
时,彩电单价为3100元,每天销售30台,营业额为![]() 元,
元,
∴每台彩电的销售价是3000元时,彩电的销售量和营业额较高.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=a(x﹣m)2﹣m+1(a、m为常数且a<0),下列结论:
①这个函数图象的顶点始终在直线y=﹣x+1上;
②a(x-1)(x+3)=﹣1有两个根x1和x2,且x1<x2,则﹣3<x1<x2<1;
③点A(x1,y1)与点B(x2,y2)在函数图象上,若x1<x2,x1+x2≥2m,则y1≤y2;
④当﹣1<x<2时,y随x的增大而增大,则m的取值范围为m≥2.
其中正确结论的序号是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(-3,2),B(-1,4),C(0,2).
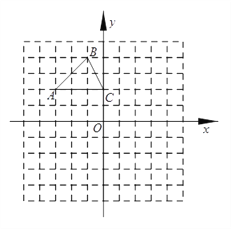
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;
(2)平移△ABC,若A的对应点A2的坐标为(-5,-2),画出平移后的△A2B2C2;
(3)若将△A2B2C2绕某一点旋转可以得到△A1B1C,请直接写出旋转中心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,若干个半径为3个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为每秒3个单位长度,点在弧线上的速度为每秒π个单位长度,则2020秒时,点P的坐标是( )
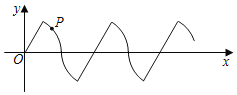
A.(2020,0)B.(3030,0)C.( 3030,![]() )D.(3030,﹣
)D.(3030,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接疫情彻底结束后的购物高峰,某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)不少于21700元,且甲种运动鞋的数量不超过100双,问该专卖店共有几种进货方案?
(3)在(2)的条件下,专卖店准备对甲种运动鞋进行优惠促销活动,决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣,某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
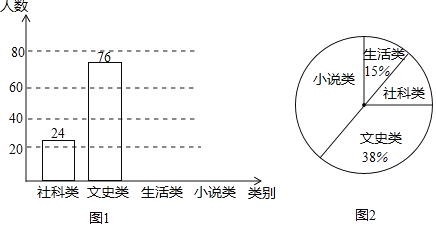
(1)此次共调查了 名学生;
(2)将条形统计图1补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2000人,估计该校喜欢“社科类”书籍的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
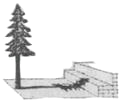
A.6.93米B.8米C.11.8米D.12米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为点D,其图象与x轴的交点A,B的横坐标分别为﹣1和3,给出下列结论:①2a﹣b=0;②a+b+c<0;③3a+c=0;④当a=![]() 时,△ABD是等腰直角三角形.其中,正确的结论有( )
时,△ABD是等腰直角三角形.其中,正确的结论有( )
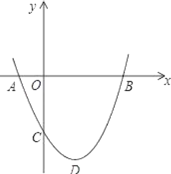
A.①②③B.③④C.②③④D.②④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com