【题目】
特例研究：如图
，等边
的边长为8，求等边的高．
经验提升：
如图
，在中，
，点P为射线BC上的任一点，过点P作
，
，垂足分别为D、E，过点C作
，垂足为
补全图形，判断线段PD，PE，CF的数量关系，并说明理由．
综合应用：
如图
，在平面直角坐标系中有两条直线
：
，
：
，若线段BC上有一点M到的距离是1，请运用中的结论求出点M的坐标．
【答案】(1)
；(2)见解析;(3)
坐标为
．
【解析】
利用等边三角形的性质和勾股定理即可得出结论；
利用面积法可以证明结论；
连接AP，同理利用
与
面积之差等于
的面积可以证得结论；
根据题意得到
，
，
，
，根据图的结论，求得M到AC的距离，即M点的纵坐标，再代入
的解析式可求出M的坐标．
解：如图
，过点A作
于G，
是等边三角形，
，
在
中，
，
，
则等边的高为；当点P在边BC上时，
，
理由如下：如图，连接AP，
，
，
，
，
，
，
，
，
，
；当点P在BC的延长线上时，
，
理由如下：如图
，连接AP，
，，，，，，
，
，，
；如图
，由题意可求得
，
，
，
，，
，，
过M分别作
轴，
，垂足分别为P、Q，
上的一点M到
的距离是1，
，
由图的结论得：
，
，
点的纵坐标为2，
在直线
，
当
时，
，坐标为．
阅读快车系列答案科目：初中数学 来源： 题型：
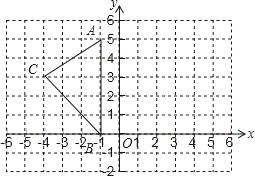
【题目】如图：在平面直角坐标系中，A（﹣1，5），B（﹣1，0），C（﹣4，3）．
（1）S△ABC＝ ．
（2）在图中作出△ABC关于y轴的对称图形△A1B1C1（其中点A、B、C的对称点分别为点A1、B1、C1）．
（3）写出点A1、B1、C1的坐标．A1 ，B1 ，C1 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，已知直线y＝﹣
x+4与x轴、y轴分别交于A、B两点，点C(0，n)是y轴上一点．把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】2019年元旦期间，某超市打出促销广告，如下表所示：
一次性所购物品的原价 | 优惠办法 |
不超过200元 | 没有优惠 |
超过200元，但不超过600元 | 全部按九折优惠 |
超过600元 | 其中600元仍按九折优惠，超过600元部分按8折优惠 |
（1）小张一次性购买物品的原价为400元，则实际付款为 元；
（2）小王购物时一次性付款580元，则所购物品的原价是多少元？
（3）小赵和小李分别前往该超市购物，两人各自所购物品的原价之和为1200元，且小李所购物品的原价高于小赵，两人实际付款共1074元，则小赵和小李各自所购物品的原价分别是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校八年级学生开展跳绳比赛活动，每班派5名学生参加，按团体总分多少排列名次，统计发现成绩最好的甲班和乙班总分相等，下表是甲班和乙班学生的比赛数据
单位：个
选手 | 1号 | 2号 | 3号 | 4号 | 5号 | 总计 |
甲班 | 100 | 98 | 105 | 94 | 103 | 500 |
乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
此时有学生建议，可以通过考察数据中的其他信息作为参考，请解答下列问题：
求两班比赛数据中的中位数，以及方差；
请根据以上数据，说明应该定哪一个班为冠军？为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，CD∥AB，OE平分∠AOD，OF⊥OE，OG⊥CD，∠CDO＝50°，则下列结论：
① ∠AOE＝65°；② OF平分∠BOD；③ ∠GOE＝∠DOF；④ ∠AOE＝∠GOD，其中正确结论的个数是（ ）
A. 4个B. 3个C. 2个D. 1个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是菱形，AB＝4，且∠ABC＝∠ABE＝60°，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则AM+BM+CM的最小值为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，在正方形ABCD外取一点E，连接AE、BE、DE．过点A作AE的垂线交DE于点P．若AE=AP=1，PB=
．下列结论：①△APD≌△AEB；②点B到直线AE的距离为
；③EB⊥ED；④S△APD+S△APB=1+
；⑤S正方形ABCD=4+．其中正确结论的序号是（ ）
A.①③④ B．①②⑤ C．③④⑤ D．①③⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AD∥BC，若∠ADP＝∠α，∠BCP＝∠β，射线OM上有一动点P．
（1）当点P在A，B两点之间运动时，∠CPD与∠α、∠β之间有何数量关系？请说明理由
（2）如果点P在A、B两点外侧运动时（点P与点A、B、O三点不重合），请你直接写出∠CPD与∠α、∠β之间的何数量关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com