
【题目】在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠,分别在BC、AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG= ![]() ,A′G=6,C′G=1,则矩形纸片ABCD的周长为 .
,A′G=6,C′G=1,则矩形纸片ABCD的周长为 . 
【答案】62
【解析】解:延长BA′交CD于M,作MN⊥C′D于N,如图所示: 
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AD=BC,AB=CD,
由折叠的性质得:∠C′=∠C=90°,∠A′=∠A=90°,CE=C′E,AB=A′B,∠CDE=∠C′DE,∠CED=∠C′ED,∠ABF=∠A′BF,∠AFB=∠A′FB,
在△ABF和△CDE中, ,
,
∴△ABF≌△CDE(SAS),
∴∠ABF=∠CDE,∠CED=∠AFB,
∴∠BEG=∠DFH,∠EBG=∠FDH,
∵CE=AF,
∴BE=DF,
在△BEG和△DFH中, ,
,
∴△BEG≌△DFH(ASA),
∴∠BGE=∠DHF,
∵∠A′GC′=∠BGE,∠A′HC′=∠DHF,
∴∠BGE=∠DHF=∠A′HC′=∠A′GC′=(360°﹣90°﹣90°)÷2=90°,
∴四边形MNC′G是矩形,
∴MN=C′G=1,∠GMN=90°,
∴∠DMN=∠EBG,
∵tan∠EBG= ![]() ,
,
∴设EG=3x,BG=4x,则BE=5x,
∴CE=C′E=3x+1,CD=AB=A′B=4x+6,
∵tan∠DMN= ![]() =tan∠EBG=
=tan∠EBG= ![]() ,MN=1,
,MN=1,
∴DN= ![]() ,
,
∴DM= ![]() ,
,
∵tan∠EBG= ![]() =
= ![]() ,
,
即 ![]() ,解得:x=2,
,解得:x=2,
∴AB=CD=14,AD=BC=17,
∴矩形ABCD的周长=2×(14+17)=62.
故答案为:62.
延长BA′交CD于M,作MN⊥C′D于N,由矩形的性质得出∠A=∠C=90°,AD=BC,AB=CD,由折叠的性质得出∠C′=∠C=90°,∠A′=∠A=90°,CE=C′E,AB=A′B,∠CDE=∠C′DE,∠CED=∠C′ED,∠ABF=∠A′BF,∠AFB=∠A′FB,由SAS证明△ABF≌△CDE(SAS),得出∠ABF=∠CDE,∠CED=∠AFB,由ASA证明△BEG≌△DFH,得出∠BGE=∠DHF,证出四边形MNC′G是矩形,得出MN=C′G=1,∠GMN=90°,设EG=3x,BG=4x,则BE=5x,CE=C′E=3x+1,CD=AB=A′B=4x+6,由三角函数求出DN= ![]() ,由勾股定理得出DM=
,由勾股定理得出DM= ![]() ,再由三角函数得出方程,解方程求出x=2,得出AB=CD=14,AD=BC=17,即可得出矩形ABCD的周长.
,再由三角函数得出方程,解方程求出x=2,得出AB=CD=14,AD=BC=17,即可得出矩形ABCD的周长.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点A1 , A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1 , A3B2∥A2B1 , A3B3∥A2B2 , A4B3∥A3B2 , ….若△A2B1B2和△A3B2B3的面积分别为1、9,则△A1007B1007A1008的面积是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD,AB=a,BC=b,且b<a<2b,则∠ADC的平分线DE折叠纸片,点A落在CD边上的点F处,再沿∠BEF的平分线EG折叠纸片,点B落在EF边上的点H处,则四边形CGHF的周长是( )
A.2a
B.2b
C.2(a﹣b)
D.a+b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°. 
(1)求证:DF∥AB;
(2)若OC=CE,BF= ![]() ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,OA=5,AB与⊙O相切于点B,BP的延长线交直线l于点C. 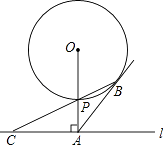
(1)求证:AB=AC.
(2)若PC=2 ![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对△ABC,D是BC边上一点,连结AD,当 ![]() =
= ![]() 时,称AD为BC边上的“平方比线”.同理AB和AC边上也存在类似的“平方比线”.
时,称AD为BC边上的“平方比线”.同理AB和AC边上也存在类似的“平方比线”. 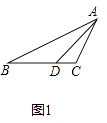
(1)如图2,△ABC中,∠BAC=RT∠,AD⊥BC于D.
证明:AD为BC边上的“平方比线”;
(2)如图3,在平面直角坐标系中,B(﹣4,0),C(1,0),在y轴的正半轴上找一点A,使OA是△ABC中BC边上的“平方比线”.
①求出点A的坐标;
②如图4,以M( ![]() ,0)为圆心,MA为半径作圆,在⊙M上任取一点P(与x轴交点除外)吗,连结PB,PC,PO.求证:PO始终是△PBC中BC边上的“平方比线”.
,0)为圆心,MA为半径作圆,在⊙M上任取一点P(与x轴交点除外)吗,连结PB,PC,PO.求证:PO始终是△PBC中BC边上的“平方比线”.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点A,B分别是二次函数y=2x2的图象上的两个点,A、B的横坐标分别为a,b(a<0,b>0),点P(0,t)是抛物线对称轴上的任意一点.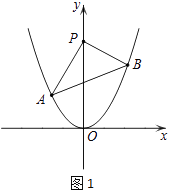
(1)当a+b=0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形?若存在,请直接写出t、a、b的其中一组值;若不存在,请说明理由;
(2)当a+b≠0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形?若存在,请写出t的取值范围,并用含t的代数式表示a2+b2的值;若不存在,请说明理由;
(3)如图2作边长为4的正方形ACDE(A、C、D、E按逆时针排列),使得AC∥x轴,若边CD与二次函数的图象总有交点,求a的取值范围.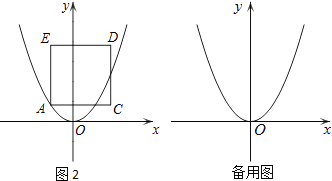
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.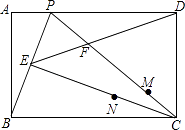
(1)求证:△ABP∽△ECB;
(2)若点E恰好为BP的中点,且AB=3,AP=k(0<k<3).
①求 ![]() 的值(用含k的代数式表示);
的值(用含k的代数式表示);
②若M、N分别为PC,EC上的任意两点,连接NF,NM,当k= ![]() 时,求NF+NM的最小值.
时,求NF+NM的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com