
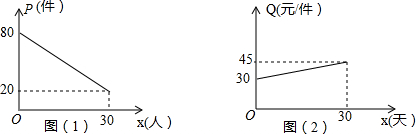
���� ��1����P=kx+80������30��20����������k��ֵ���ó���������P������������ʱ��x���죩֮��ĺ�����ϵʽ����Q=mx+30������30��45����������m��ֵ���ó�Q��Ԫ/����������ʱ��x���죩�ĺ�����ϵʽ��
��2���������������еĻ���������ϵ����������=������������һ�������ۼ�-һ���Ľ��ۣ�������������ϵʽ��
��3������2���к�����ϵʽ�䷽�ɵ��䶥��ʽ������Ա���x�ķ�Χ�����ݶ��κ��������ʿɵú�������ֵ�����
��� �⣺��1����P=kx+80������30��20�����룬
��20=30k+80�����k=-2��
������������P������������ʱ��x���죩֮��ĺ�����ϵʽΪP=-2x+80��
��Q=mx+30������30��45�����룬
��45=30m+30�����m=$\frac{1}{2}$��
����Q��Ԫ/����������ʱ��x���죩�ĺ�����ϵʽΪQ=$\frac{1}{2}$x+30��
�ʴ�ΪP=-2x+80��Q=$\frac{1}{2}$x+30��
��2���������⣬��W=P��Q-20��=��-2x+80��[��$\frac{1}{2}$x+30��-20]=-x2+20x+800��1��x��30����xΪ����������
��W=-x2+20x+800��
��3����w=-x2+20x+800=-��x-10��2+900��
�൱x=10ʱ��Wȡ���ֵΪ900��
����30��������У���10�����������������������Ϊ900Ԫ��
���� ���⿼���˶��κ�����Ӧ�ã�����ϵ������һ�κ����Ľ���ʽ������Ӫ�������еĻ���������ϵ����������ϵʽ�ǽ���ؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
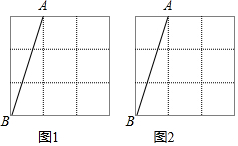
 ��ͼ��С�ָ�ס�ĵ����������ǣ�������
��ͼ��С�ָ�ס�ĵ����������ǣ�������| A�� | ��3��3�� | B�� | ��-4��5�� | C�� | ��-4��-6�� | D�� | ��3��-6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com