
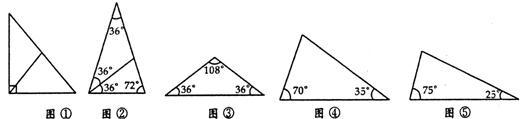
我们知道:直角三角形斜边上的中线等于斜边的一半,说明斜边上的中线可把直角三角形分成两个等腰三角形(图①)。又比如,顶角为36°的等腰三角形也能分成两个等腰三角形(图②)。
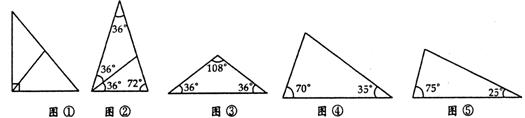
1.试试看,你能把图③、图④、图⑤中的三角形分成两个等腰三角形吗
2.△ABC中,有一内角为36°,过某一顶点的直线将△ABC分成两个等腰三角形,则满足上述条件的不同形状(相似的认为是同一形状)的△ABC最多有5种,除了图②、图③中的两种,还有三种,请你画出来
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 知线段AB=1,∠BAC=θ.
知线段AB=1,∠BAC=θ.查看答案和解析>>
科目:初中数学 来源: 题型:
 通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=
通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sadA=| 底边 |
| 腰 |
| BC |
| AB |
| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,也可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A=| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 5 |
2-2
|
2-2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| 底边 |
| 腰 |
| BC |
| AB |
| 3 |
| 3 |
| 8 |
| 5 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com