
【题目】如图,在平面直角坐标系中,直线![]() 的解析式为
的解析式为![]() ,点
,点![]() 的坐标分别为(1,0),(0,2),直线
的坐标分别为(1,0),(0,2),直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
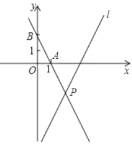
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 在第一象限的直线
在第一象限的直线![]() 上,连接
上,连接![]() ,且
,且![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)y=2x+2;(2)![]()
【解析】
(1)利用待定系数法即可得到直线AB的表达式;
(2)通过解方程组即可得到点P的坐标,设点Q(t,2t6),作QH⊥x轴,垂足为H,PK⊥x轴,垂足为K.可得KA=21=1,PK=2,HA=t1,QH=2t6,根据勾股定理得到AP,AQ,根据AP=AQ得到关于t的方程,解方程求得t,从而得到点Q的坐标.
解:(1)设AB的解析式为y=kx+b(k≠0),
把(1,0)、(0,2)代入y=kx+b
得:![]() ,解得:k=2,b=2,
,解得:k=2,b=2,
∴y=2x+2;
(2)联立得![]() ,解得:x=2,y=2,
,解得:x=2,y=2,
∴P(2,2),
设点Q(t,2t6),作QH⊥x轴,垂足为H.PK⊥x轴,垂足为K.
KA=21=1,PK=2,HA=t1,QH=2t6
AP=![]() ,AQ=
,AQ=![]() ,
,
∵AP=AQ,
∴(t1)2+(2t6)2=5,
解得:t1=2(舍去);t2=![]() ,,
,,
把x=![]() 代入y=2x6,得y=
代入y=2x6,得y=![]() ,
,
∴![]() .
.



 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
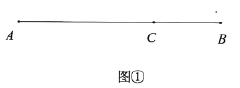
【题目】2019年6月12日,重庆直达香港高铁的车票正式开售据悉,重庆直达香港的这趟G319/320次高铁预计在7月份开行,全程1342公里只需7个半小时该车次沿途停靠站点包括遵义、贵阳东、桂林西、肇庆东、广州南和深圳北重庆直达香港高铁开通将为重庆旅游业发展增添生机与活力,预计重庆旅游经济将创新高在此之前技术部门做了大量测试,在一次测试中一高铁列车从![]() 地出发匀速驶向
地出发匀速驶向![]() 地,到达
地,到达![]() 地停止;同时一普快列车从
地停止;同时一普快列车从![]() 地出发,匀速驶向
地出发,匀速驶向![]() 地,到达
地,到达![]() 地停止且
地停止且![]() ,
,![]() 两地之间有一
两地之间有一![]() 地,其中
地,其中![]() ,如图①两列车与
,如图①两列车与![]() 地的距离之和
地的距离之和![]() (千米)与普快列车行驶时间
(千米)与普快列车行驶时间![]() (小时)之间的关系如图②所示则高铁列车到达
(小时)之间的关系如图②所示则高铁列车到达![]() 地时,普快列车离
地时,普快列车离![]() 地的距离为__________千米.
地的距离为__________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
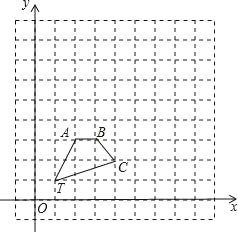
【题目】如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).
(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;
(2)写出点A′,B′,C′的坐标:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,(1)数轴上的所有点都表示有理数;(2)无理数可以用数轴上的点表示;(3)实数与数轴上的点一一对应;(4)无限小数是无理数;(5)带根号的数都是无理数;(6)数轴上的点不是表示有理数,就是表示无理数;错误命题的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
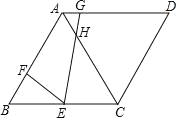
【题目】如图,在菱形ABCD中,∠B=60°,BC=6,E为BC中点,F是AB上一点,G为AD上一点,且BF=2,∠FEG=60°,EG交AC于点H,下列结论:①△BEF∽△CHE;②AG=1;③EH=![]() ;④S△BEF=3S△AGH;正确的是______.(填序号即可)
;④S△BEF=3S△AGH;正确的是______.(填序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列三个结论:①AP=EF;②△APD一定是等腰三角形;③∠PFE=∠BAP.其中正确结论的序号是( )
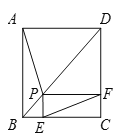
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末,历史老师为了了解所任教的甲、乙两班学生的历史基础知识背诵情况,从甲、乙两个班学生中分别随机抽取了20名学生来进行历史基础知识背诵检测,满分50分,得到学生的分数相关数据如下:
甲 | 32 | 35 | 46 | 23 | 41 | 49 | 37 | 41 | 36 | 41 |
37 | 44 | 39 | 46 | 46 | 41 | 50 | 43 | 44 | 49 |
乙 | 25 | 34 | 43 | 46 | 35 | 41 | 42 | 46 | 44 | 42 |
47 | 45 | 42 | 34 | 39 | 47 | 49 | 48 | 45 | 42 |
通过整理,分析数据:两组数据的平均数、中位数、众数如下表:
平均数(分) | 中位数(分) | 众数(分) | |
甲 | 41 | 41 |
|
乙 | 41.8 |
| 42 |
历史老师将乙班成绩按分数段(![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 表示分数)绘制成扇形统计图,如图(不完整)
表示分数)绘制成扇形统计图,如图(不完整)
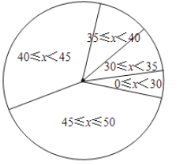
请回答下列问题:
(1)![]() _______分;
_______分;
(2)扇形统计图中,![]() 所对应的圆心角为________度;
所对应的圆心角为________度;
(3)请结合以上数据说明哪个班背诵情况更好(列举两条理由即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com