
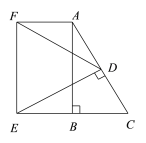
【题目】Rt△ABC中,∠ABC=90°,∠C=60°,BC=2,D是AC的中点,从D作DE⊥AC与CB的延长线交于点E,以AB、BE为邻边作矩形ABEF,连结DF,则DF的长是( )
A. 4![]() B. 3
B. 3![]() C. 2
C. 2![]() D. 4
D. 4
【答案】C
【解析】
由已知条件易证BC=![]() AC=CD,这样结合∠EDC=∠ABC=90°,∠C=∠C,即可证得△EDC≌△ABC,结合四边形ABEF是矩形可得DE=AB=EF,再证∠DEF=60°即可得到△DEF是等边三角形,从而可得DF=DE,这样在Rt△DEC中由DC=BC=2结合∠C=60°求出DE的长即可得到DF的长.
AC=CD,这样结合∠EDC=∠ABC=90°,∠C=∠C,即可证得△EDC≌△ABC,结合四边形ABEF是矩形可得DE=AB=EF,再证∠DEF=60°即可得到△DEF是等边三角形,从而可得DF=DE,这样在Rt△DEC中由DC=BC=2结合∠C=60°求出DE的长即可得到DF的长.
∵在△ABC中,∠ABC=90°,∠C=60°,
∴∠BAC=30°,
∴BC=![]() AC,
AC,
又∵点D是AC的中点,
∴BC=DC,
∵DE⊥AC,
∴∠EDC=90°=∠ABC,
又∵∠C=∠C,
∴△EDC≌△ABC,
∴DE=AB,∠DEC=∠BAC=30°,
∵四边形ABEF是矩形,
∴DE=AB=EF,∠FEC=90°,
∴∠FED=90°-30°=60°,
∴△DEF是等边三角形,
∴DF=DE,
∵在Rt△DEC中,∠DEC=30°,∠EDC=90°,CD=2,
∴CE=4,
∴DE=![]() ,
,
∴DF=![]() .
.
故选C.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:
【题目】某校九年级10个班师生举行毕业文艺汇演,每班2个节目,有歌唱与舞蹈两类节目,年级统计后发现歌唱类节目数比舞蹈类节目数的2倍少4个.
(1)九年级师生表演的歌唱与舞蹈类节目数各有多少个?
(2)该校七、八年级师生有小品节目参与,在歌唱、舞蹈、小品三类节目中,每个节目的演出平均用时分别是5分钟、6分钟、8分钟,预计所有演出节目交接用时共花15分钟.若从20:00开始,22:30之前演出结束,问参与的小品类节目最多能有多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数y= ![]() (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2. 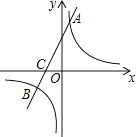
(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
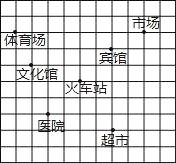
【题目】如图,这是某市部分简图,为了确定各建筑物的位置:
(1)请你以火车站为原点建立平面直角坐标系.
(2)写出市场的坐标为 ;超市的坐标为 .
(3)请将体育场为A、宾馆为C和火车站为B看作三点用线段连起来,得△ABC,然后将此三角形向下平移4个单位长度,画出平移后的△A1B1C1,并求出其面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件:_____________,使△AEH≌△CEB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
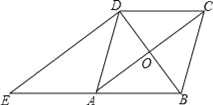
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
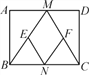
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.
(1)求证:△ABM≌△DCM;
(2)当AB∶AD=___时,四边形MENF是正方形,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com