
分析 (1)过点A(a,3)作AE⊥x轴于点E,则AE=3,根据三角形的面积公式即可得到结论;
(2)由a=$\sqrt{7}$,得到A($\sqrt{7}$,3),B($\sqrt{7}$+4,3),由于yA=yB,得到AB∥OC,推出四边形OABC是平行四边形,根据勾股定理得到OE=$\sqrt{O{E}^{2}+A{E}^{2}}$=4,于是得到四边形OABC是菱形;
(3)由点P是线段OB上任意一点,得到当点P与点O重合时,所对应的P'(2,1)在射线OB上,设直线OB的解析式为y=kx,得到线段OB解析式为y=$\frac{1}{2}$x.求得B(6,3),若线段OB上存在点G(x,$\frac{1}{2}$x),使得△OGC为等腰三角形,则可分为下列三种情形进行讨论:①当OG=GC时,②当OG=OC=4时,③当GC=OC=4时,于是得到结论.
解答 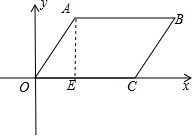 解:(1)过点A(a,3)作AE⊥x轴于点E,则AE=3,
解:(1)过点A(a,3)作AE⊥x轴于点E,则AE=3,
又∵C(4,0)
∴OC=4,
∴S△OAC=$\frac{1}{2}$•OC•AE=6;
(2)若a=$\sqrt{7}$,则A($\sqrt{7}$,3),B($\sqrt{7}$+4,3),
∵yA=yB,
∴AB∥OC,
AB=4,OC=4,
∴AB=OC,
∴四边形OABC是平行四边形,
∵∠AEO=90°,AE=3,OE=$\sqrt{O{E}^{2}+A{E}^{2}}$=4,
∴OA=AB,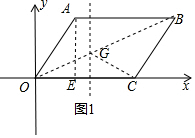
∴四边形OABC是菱形;
(3)∵点P是线段OB上任意一点,
∴当点P与点O重合时,
所对应的P'(2,1)在射线OB上,
设直线OB的解析式为y=kx,代入得,
∴k=$\frac{1}{2}$,
∴线段OB解析式为y=$\frac{1}{2}$x.
∵B(a+4,3)在直线OB上,
∴a+4=6,
∴B(6,3),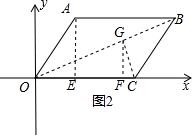
若线段OB上存在点G(x,$\frac{1}{2}$x),使得△OGC为等腰三角形,则可分为下列三种情形进行讨论:
①当OG=GC时,如图1,点G在OC的垂直平分线上,
则有x=2,
∴此时G(2,1)在线段OB上,
②当OG=OC=4时,
过点G作GF⊥x轴于点F,
则∠AFG=90°,x2+($\frac{1}{2}$x)2=42,
∴x=$\frac{8\sqrt{5}}{5}$<6,
∴G($\frac{8\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$)在线段OB上;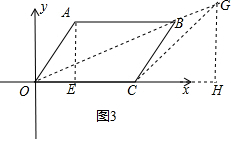
③当GC=OC=4时,
过点G作GH⊥x轴于点H,
则∠GHO=90°,(x-4)2+($\frac{1}{2}$x)2=42,
∴x=$\frac{32}{5}$>6,
∴此时点G不在线段OB上.
综上所述,符合条件的点G的坐标为(2,1)或($\frac{8\sqrt{5}}{5}$,$\frac{4\sqrt{5}}{5}$).
点评 本题考查了平行四边形的判定和性质,菱形的判定,勾股定理,等腰三角形的性质,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
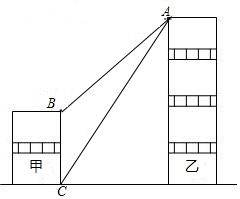 小颖站在自家阳台的A处用测角仪观察对面的商场,如图,在A处测得商场楼顶B点的俯角为45°,商场楼底C点的俯角为60°,若商场高17.6米,小颖家所在楼房每层楼的平均高度为3米,则小颖家住在几楼?小颖家与商场相距多少米?(结果保留整数,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)
小颖站在自家阳台的A处用测角仪观察对面的商场,如图,在A处测得商场楼顶B点的俯角为45°,商场楼底C点的俯角为60°,若商场高17.6米,小颖家所在楼房每层楼的平均高度为3米,则小颖家住在几楼?小颖家与商场相距多少米?(结果保留整数,参考数据:$\sqrt{3}$≈1.732,$\sqrt{2}$≈1.414)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
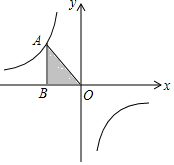 如图,已知反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=-2.
如图,已知反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象经过点A,过A点作AB⊥x轴,垂足为B.若△AOB的面积为1,则k=-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
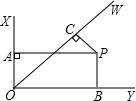 如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )
如图,∠XOY=90°,OW平分∠XOY,PA⊥OX,PB⊥OY,PC⊥OW,其中A,B,C为垂足,若OA+OB+OC=1,则OC=( )| A. | 2-$\sqrt{2}$ | B. | $\sqrt{2}-1$ | C. | $\sqrt{6}$-2 | D. | 2$\sqrt{3}$-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com