
【题目】读下列因式分解的过程,再回答所提出的问题:
1 x x(1 x) x(1 x)2
(1 x)[1 x x(1 x)]
(1 x)2 (1 x)
(1 x)3
(1)上述分解因式的方法是 ,共应用了 次.
(2)若分解1 x x(1 x) x(1 x)2 … x(1 x)2018,则需应用上述方法 次,结果是 .
(3)分解因式:1 x x(1 x) x(1 x)2… x(1 x)n
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】某检修小组从A地出发,在东西方向的马路上检修线路,如果规定向东行驶为正,向西行驶为负,一天中七次行驶纪录如下.(单位:km)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
-4 | +8 | -9 | +8 | +6 | -5 | -2 |
(1)求收工时距A地多远?
(2)若每km耗油0.4升,问一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
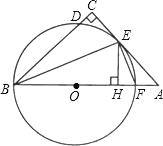
【题目】如图,在△ABC中,∠C=90°,∠ABC的平分线交AC于点E,过点E作BE的垂线交AB于点F,⊙O是△BEF的外接圆.
(1)求证:AC是⊙O的切线;
(2)过点E作EH⊥AB,垂足为H,求证:CD=HF;
(3)若CD=1,EH=3,求BF及AF长.
查看答案和解析>>
科目:初中数学 来源: 题型:
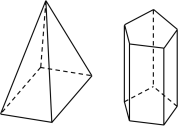
【题目】(1)下面两个立体图形的名称是:__________,__________
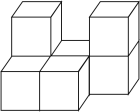
(2)一个立体图形的三视图如下图所示,这个立体图形的名称是__________

(3)画出下面立体图形的主视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数:x1,x2,x3,称为数列x1,x2,x3,计算![]() ,
,![]() ,
,![]() ,将这三个数的最小值称为数列x1,x2,x3的价值.例如,对于数列2,-1,3,因为
,将这三个数的最小值称为数列x1,x2,x3的价值.例如,对于数列2,-1,3,因为![]() ,
,![]() ,
,![]() ,所以数列2,-1,3的价值为
,所以数列2,-1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列-1,2,3的价值为![]() ;数列3,-1,2的价值为1:…经过研究,小丁发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,-1,2的价值为1:…经过研究,小丁发现,对于“2,-1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列4,3,-2的价值为______.
(2)将“4,3,-2”这三个数按照不同的顺序排列,可得到若干个数列,求这些数列的价值的最小值(请写出过程并作答).
(3)将3,-8,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为_______ (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是(A,B)的好点.
例如,如图1,点A表示的数为-1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是(A,B)的好点;
又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D就不是(A,B)的好点,但点D是(B,A)的好点.
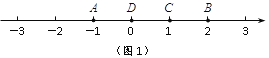
知识运用:
⑴ 如图1,点B是(D,C)的好点吗? (填是或不是);
⑵ 如图2,A、B为数轴上两点,点A所表示的数为-40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分剪下,拼成右边的矩形,由图形①到图形②的变化过程能够验证的一个等式是( )
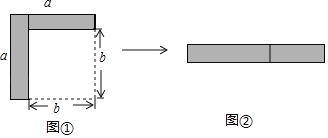
A. a(a+b)=a2+ab B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2 D. a(a﹣b)=a2﹣ab
查看答案和解析>>
科目:初中数学 来源: 题型:
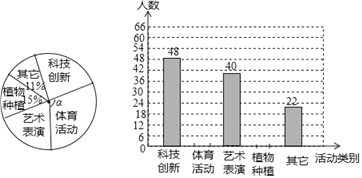
【题目】深圳市教育局在全市中小学开展“四点半活动”试点工作,某校为了了解学生参与“四点半活动”项目的情况,对初中的部分学生进行了随机调查,调查项目分为“科技创新”类,“体育活动”类,“艺术表演”类,“植物种植”类及“其它”类共五大类别,并根据调查的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息解答下面的问题.
(1)请求出此次被调查学生的总人数 人;
(2)根据以上信息,补全频数分布直方图;
(3)求出扇形统计图中,“体育活动”α的圆心角等于 度;
(4)如果本校初中部有1800名学生,请估计参与“艺术表演”类项目的学生大约多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com