
【题目】某水果店在两周内,将标价为10元/斤的某种水果,经过两次降价后的价格为8.1元/斤,并且两次降价的百分率相同.
(1)求该种水果每次降价的百分率;
(2)从第一次降价的第1天算起,第x天(x为整数)的售价、销量及储存和损耗费用的相关信息如表所示.已知该种水果的进价为4.1元/斤,设销售该水果第x(天)的利润为y(元),求y与x(1≤x<15)之间的函数关系式,并求出第几天时销售利润最大?

(3)在(2)的条件下,若要使第15天的利润比(2)中最大利润最多少127.5元,则第15天在第14天的价格基础上最多可降多少元?
【答案】(1)10%;(2)![]() ,第10天时销售利润最大;(3)0.5.
,第10天时销售利润最大;(3)0.5.
【解析】试题分析:(1)设这个百分率是x,根据某商品原价为10元,由于各种原因连续两次降价,降价后的价格为8.1元,可列方程求解;
(2)根据两个取值先计算:当1≤x<9时和9≤x<15时销售单价,由利润=(售价﹣进价)×销量﹣费用列函数关系式,并根据增减性求最大值,作对比;
(3)设第15天在第14天的价格基础上最多可降a元,根据第15天的利润比(2)中最大利润最多少127.5元,列不等式可得结论.
试题解析:解:(1)设该种水果每次降价的百分率是x,10(1﹣x)2=8.1,x=10%或x=190%(舍去).
答:该种水果每次降价的百分率是10%;
(2)当1≤x<9时,第1次降价后的价格:10×(1﹣10%)=9,∴y=(9﹣4.1)(80﹣3x)﹣(40+3x)=﹣17.7x+352,∵﹣17.7<0,∴y随x的增大而减小,∴当x=1时,y有最大值,y大=﹣17.7×1+352=334.3(元);
当9≤x<15时,第2次降价后的价格:8.1元,∴y=(8.1﹣4.1)(120﹣x)﹣(3x2﹣64x+400)=﹣3x2+60x+80=﹣3(x﹣10)2+380,∵﹣3<0,∴当9≤x≤10时,y随x的增大而增大,当10<x<15时,y随x的增大而减小,∴当x=10时,y有最大值,y大=380(元).
综上所述,y与x(1≤x<15)之间的函数关系式为: ![]() ,第10天时销售利润最大;
,第10天时销售利润最大;
(3)设第15天在第14天的价格基础上最多可降a元,由题意得:380﹣127.5≤(4﹣a)(120﹣15)﹣(3×152﹣64×15+400),252.5≤105(4﹣a)﹣115,a≤0.5.
答:第15天在第14天的价格基础上最多可降0.5元.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
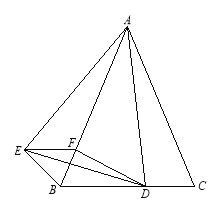
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(a,0),点B的坐标是(b,0),其中a,b满足![]() .
.
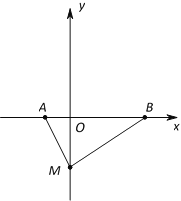
(1)填空:a=______,b=_______;
(2)在![]() 轴负半轴上有一点M(0,m),三角形ABM的面积为4.
轴负半轴上有一点M(0,m),三角形ABM的面积为4.
①求m的值;
②将线段AM沿x轴正方向平移,使得A的对应点为B,M的对应点为N. 若点P为线段AB上的任意一点(不与A,B重合),试写出∠MPN,∠PMA,∠PNB之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在CB的延长线上,点F在DE的延长线上,连接AF,分别与BD、CE交于点G、H。已知∠1=52°,∠2=128°。
(1)求证:BD∥CE;
(2)若∠A=∠F,试判断∠C与∠D的数量关系,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, ![]() ,
, ![]() 与
与![]() 成正比例,
成正比例, ![]() 与
与![]() 成反比例,并且当
成反比例,并且当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
(![]() )求
)求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(![]() )当
)当![]() 时,求
时,求![]() 的值.
的值.
【答案】(![]() )
)![]() ;(
;(![]() )
)![]() ,
, ![]() .
.
【解析】分析:(1)首先根据![]() 与x成正比例,
与x成正比例, ![]() 与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出
与x成反比例,且当x=1时,y=4;当x=2时,y=5,求出![]() 和
和![]() 与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
与x的关系式,进而求出y与x的关系式,(2)根据(1)问求出的y与x之间的关系式,令y=0,即可求出x的值.
本题解析:
(![]() )设
)设![]() ,
, ![]() ,
,
则![]() ,
,
∵当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
∴
解得, ![]() ,
,
∴![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() .
.
(![]() )把
)把![]() 代入
代入![]() 得,
得,
![]() ,
,
解得: ![]() ,
, ![]() .
.
点睛:本题考查了用待定系数法求反比例函数的解析式:(1)设出含有待定系数的反比例函数解析式y=kx(k为常数,k≠0);(2)把已知条件(自变量与对应值)代入解析式,得到待定系数的方程;(3)解方程,求出待定系数;(4)写出解析式.
【题型】解答题
【结束】
24
【题目】如图,菱形![]() 的对角线
的对角线![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 且
且![]() ,连接
,连接![]() 、
、![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)若菱形![]() 的边长为2,
的边长为2, ![]() .求
.求![]() 的长.
的长.
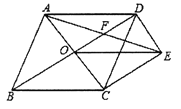
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛,初赛后对选手成绩进行了整理,分成5个小组(x表示成绩,单位:分),A组:75≤x<80;B组:80≤x<85;C组:85≤x<90;D组:90≤x<95;E组:95≤x<100.并绘制出如图两幅不完整的统计图.

请根据图中信息,解答下列问题:
(1)参加初赛的选手共有 名,请补全频数分布直方图;
(2)扇形统计图中,C组对应的圆心角是多少度?E组人数占参赛选手的百分比是多少?
(3)学校准备组成8人的代表队参加市级决赛,E组6名选手直接进入代表队,现要从D组中的两名男生和两名女生中,随机选取两名选手进入代表队,请用列表或画树状图的方法,求恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成下列各题:平面内的两条直线有相交和平行两种位置关系。


(1)如图1,若![]() ,点P在AB,CD之间,求证:∠BPD=∠B+∠D;
,点P在AB,CD之间,求证:∠BPD=∠B+∠D;
(2)在图1中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图2,请写出![]() ,∠B,
,∠B,![]() ,
,![]() 之间的数量关系并说明理由;
之间的数量关系并说明理由;
(3)利用(2)的结论,求图3中![]() +∠G=n×90°,则n=____.
+∠G=n×90°,则n=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:
![]()
(1)若企业销售该产品获得的利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD是正方形,点E、F分别是BC、CD边的中点,连结AE、BF交于点P,连结DP.
(1)求证:AE⊥BF.
(2)求证:PD=AB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com